2.2.14 Локально сглаженная функция
Данный метод создает функцию, которая является сглаженным представлением заданной исходной функции. Аргументы созданной функции совпадают с аргументами исходной функции. Сглаживание производится в локальной окрестности значений аргументов функции. Размер окрестности сглаживания задается отдельно для каждого аргумента функции. Производные функции определяются численным методом. Функция, созданная данным методом, считается дифференцируемой три раза по любому ее аргументу или произвольной комбинации аргументов. Вид локально сглаженной функции представлен на Рис. 9.
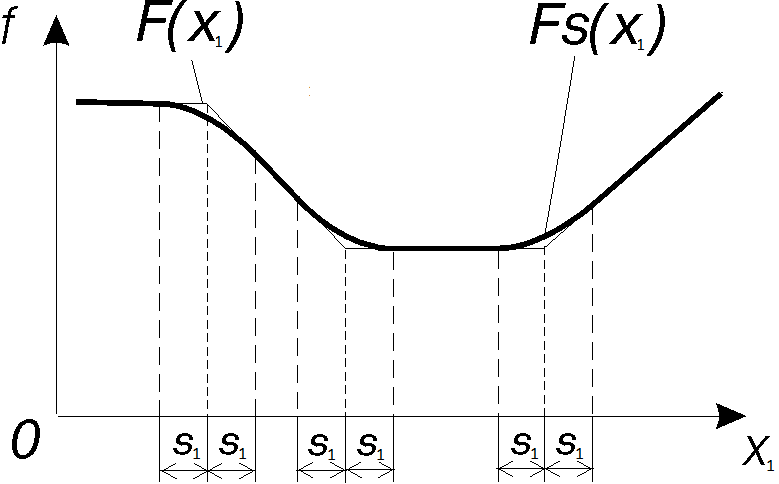
Рис. 9. Локально сглаженная функция
Обычно данный метод создания функции используется в тех случаях, когда для решения задачи требуется дифференцируемая функция, а имеющаяся для этого исходная функция не является дифференцируемой в строгом математическом понимании или записана в виде выражения с логическими условиями. Дифференцируемые функции требуются, например, при задании программных движений, определяющих положение или скорость механической системы, при задании контактных шарниров и в других случаях. Примером не дифференцируемой функции является функция по точкам с линейной аппроксимацией.
Синтаксис метода создания
localSmooth(F, list(s1, s2, ...) )
Обязательные позиционные параметры метода
function F
Заданная исходная функция.
list(scalar s1, scalar s2, ...)
Значения размеров окрестности сглаживания функции. Для каждого аргумента функции F задается собственное значение размера окрестности сглаживания. Порядок скаляров в списке соответствует порядку аргументов функции F.
Описание
В случае одного аргумента значения локально сглаженной функции и ее производных определяется следующим образом:
;
;
;
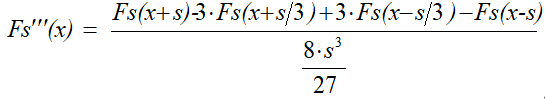,где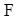 
– заданная исходная функция; 
– значение аргумента; 
– значение размера окрестности сглаживания функции, n – число интервалов разбиения окрестности сглаживания.
– заданная исходная функция; 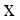– значение аргумента; 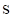– значение размера окрестности сглаживания функции, n – число интервалов разбиения окрестности сглаживания.Если функция имеет несколько аргументов, то ее значение определяется следующим образом:
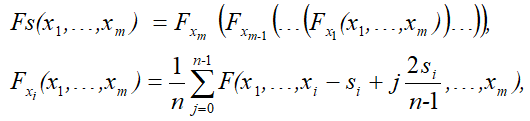
где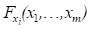 
– значение локально сглаженной функции при сглаживании исходной функции по 
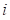-му аргументу как функции одного этого аргумента; 
- значение размера окрестности сглаживания функции по -му аргументу; 
– число аргументов функции.
– значение локально сглаженной функции при сглаживании исходной функции по -му аргументу как функции одного этого аргумента; - значение размера окрестности сглаживания функции по 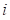-му аргументу; 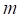– число аргументов функции.Значения производных локально сглаженной функции нескольких аргументов определяются последовательным численным дифференцированием по аргументам. Для этого используются те же формулы, что и при определении производных функции одного аргумента, но вместо значений исходной функции в правой части формул используются значения производных локально сглаженной функции при дифференцировании по аргументам, стоящим перед текущим аргументом дифференцирования.