2.2.8 Функция по точкам
Функция имеет один аргумент. Значение функции задается списком точек (значение аргумента, значение функции). Значения функции в заданных точках соответствуют этому списку. Значения вне заданной сетки точек определяются в соответствии с указанным методом аппроксимации. Вид функции представлен на Рис. 4.
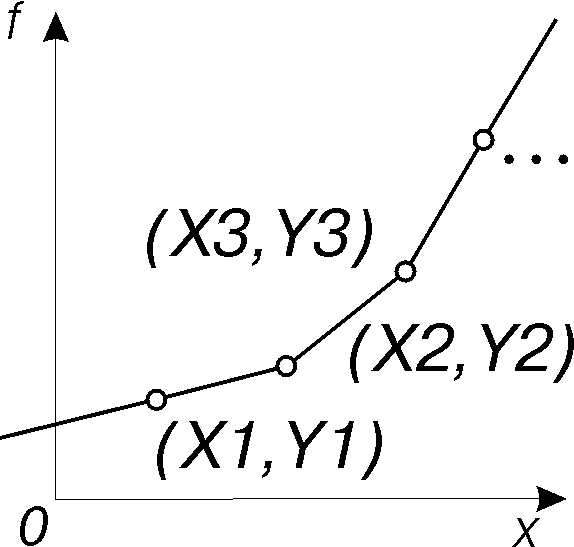
Рис. 4. Функция по точкам
Синтаксис метода создания
pieceLine(list((X1, Y1),…), approximation =…)
Обязательные позиционные параметры метода
list((scalar X1, scalar Y1),…)
Список заданных точек функции. Каждая точка представляет собой два скаляра (Xi, Yi), где Xi - значение аргумента; Yi - значение функции при значении аргумента, равном Xi.
Необязательные именованные параметры метода
approximation = [interpolateC0:/ interpolateC2:/ interpolateC3:/ interpolateAkimaC1:/ interpolateAkimaC2:]
Метод аппроксимации для определения значения функции вне заданной сетки точек. По умолчанию approximation= interpolateC0:.
approximation = interpolateC0:Для определения значения функции вне заданной сетки точек используется линейная интерполяция. При этом сохраняется непрерывность самой функции, но не ее производных.
approximation = interpolateC2:Для определения значения функции вне заданной сетки точек используется сплайновая интерполяция степенными функциями третьего порядка. При этом сохраняется непрерывность самой функции и всех ее производных до второй включительно.
approximation = interpolateC3:Для определения значения функции вне заданной сетки точек используется сплайновая интерполяция степенными функциями четвертого порядка. При этом сохраняется непрерывность самой функции и всех ее производных до третьей включительно.
approximation = interpolateAkimaC1:Для определения значения функции вне заданной сетки точек используется сплайновая интерполяция третьего порядка по методу Акимы. При этом сохраняется непрерывность самой функции и ее первой производной.
approximation = interpolateAkimaC2:Для определения значения функции вне заданной сетки точек используется сплайновая интерполяция пятого порядка по методу Акимы. При этом сохраняется непрерывность самой функции и всех ее производных до второй включительно.
Описание
Число точек, задающих функцию, не должно быть меньше двух. Точки задания функции в списке могут быть перечислены в произвольном порядке, поскольку их упорядочивание по значению аргумента производится автоматически после завершения создания списка.
Для совместимости точек задания функции в данном методе необходимо:
− совпадение размерностей значений аргументов Xi всех точек списка;
− совпадение размерностей значений функции Yi всех точек списка.
При использовании методов сплайновой интерполяции, обеспечивается непрерывность функции и ее производных до указанного порядка. Граничные условия при решении задачи аппроксимации берутся свободными. Значения производных функции на границах заданного интервала не фиксируются.