3.1.17 Точка касания окружность-прямая-окружность
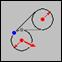Данный метод создает точку касания окружности и прямой. Прямая является касательной к двум окружностям. Точка касания строится на первой окружности радиуса R1 и центром в точке Center1. Прямая может быть как внешней, так и внутренней касательной к двум окружностям. Окружности и прямая лежат в плоскости, нормаль которой определяется вектором Vector.
Рис. 28. Точка касания окружность-прямая-окружность
Синтаксис метода создания
tangentCC(Center1, R1, Center2, R2, Vector, tangentSide=…, pointStyle=..., color=..., visible=...)
Обязательные позиционные параметры метода
point Center1
Центр первой окружности.
scalar R1 [length]
Радиус первой окружности.
point Center2
Центр второй окружности.
scalar R2 [length]
Радиус второй окружности.
vector Vector
Вектор, определяющий нормаль плоскости построения окружностей и прямой.
Необязательные именованные параметры метода
tangentSide = [tangentExternal:/tangentInternal:]
Параметр определяет тип касательной. По умолчанию tangentSide = tangentExternal:.
tangentSide = tangentExternal:Прямая является касательной к окружностям с внешней стороны.
tangentSide = tangentInternal:Прямая является касательной к окружностям с внутренней стороны.
Параметры являются общими для всех методов создания геометрических объектов и описаны в пункте «Необязательные именованные параметры объектов» общей части главы «Геометрические и массово-инерционные объекты».
Описание
При построении точки касания окружности и прямой создается вспомогательный узел OXYZ. Ось X совпадает с вектором, направленным из точки Center1 в точку Center2. Ось Y определяется как векторное произведение заданного вектора Vector и оси X. Ось Z дополняет узел до правой системы координат.
Ось Z вспомогательного узла является нормалью к плоскости построения окружностей и прямой. Точка касания строится на первой окружности в стороне оси Y вспомогательного узла.
В общем случае первая окружность и прямая имеют две точки касания. Чтобы изменить точку касания окружности и прямой необходимо изменить направление вектора Vector на противоположное.