5.1.30 Производная переменного датчика

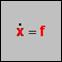Датчик предназначен для определения значения производной переменного датчика с заданным начальным значением. В этом случае значение переменного датчика определяется дифференциальным уравнением

где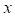

– значение переменного датчика;

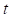– время;

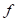– значение производной датчика по времени, которое задается данным методом производная переменного датчика. В начальный момент движения ММС (при переводе проекта из режима редактирования в режим исследования) переменный датчик равен заданному при его определении начальному значению.

Данный вид изменения значения переменного датчика в соответствии с дифференциальным уравнением может быть использован совместно с изменениями механизма обновление значения датчика или обновление значений датчиков с использованием DLL-модуля. В этом случае датчик будет мгновенно менять свое значение в моменты срабатывания соответствующего изменения механизма, а между этими моментами значение датчика будет изменяться согласно заданному дифференциальному уравнению.

Если значение производной в текущий момент не может быть вычислено, то в этот момент времени переменный датчик не имеет значения. В дальнейшем, для того чтобы значение переменного датчика вновь стало определено, необходимо чтобы было выполнено два условия:

− производная корректно определена;

− значение переменного датчика обновлено с помощью одного из соответствующих изменений механизма корректным значением.

Размерность значения датчика совпадает с размерностью указанного переменного датчика, деленной на время.

Датчик является не дифференцируемым по параметрам положения механизма.

Синтаксис метода создания

diff(x, f)

Обязательные позиционные параметры метода

sensor x

Имя переменного датчика с заданным начальным значением, для которого создаваемый датчик определяет производную по времени.

sensor f

Производная переменного датчика по времени.

Описание

Данный метод создания датчика в совокупности с методом переменный датчик с заданным начальным значением позволяет описывать различные системы дифференциальных уравнений. В качестве примера рассмотрим систему дифференциальных уравнений

;

Введя новые переменные

;

преобразуем исходную систему в форму Коши:

;

Систему дифференциальных уравнений в форме Коши можно описать с помощью переменных датчиков с заданным начальным значением и производных переменных датчиков с заданным начальным значением.

Представленная система дифференциальных уравнений в форме Коши может быть описана при моделировании следующим образом.

Пример

sensor x1=var(x10);

sensor x2=var(x20);

sensor x3=var(x30);

sensor x4=var(x40);

…

sensor x1t=diff(x1,x3);

sensor x2t=diff(x2,x4);

sensor x3t=diff(x3,-a*x3-b*x1+c*x4*x4);

sensor x4t=diff(x4, (m/k)*x3+(n/k)*x1);