6.16.4 Спектральный анализ
Теоретические основы
Спектральный анализ позволяет получить частотные характеристики физического процесса, описываемого некоторой функцией. Обычно под частотой понимают характеристику периодического процесса, равную количеству повторений или возникновения событий в единицу времени, т.е. время при таком определении является аргументом периодического процесса. В нашем случае в качестве аргумента периодического процесса может выступать не только время, но и другие физические или безразмерные величины. Так, например, частота может представлять собой число неровностей на единицу длины или число изделий заданного размера в заданном количестве изделий (подробнее смотри в разделе «Шкала спектра (spectralScale)» главы «Служебные объекты» книги «Описание объектов многокомпонентной механической системы»).
Спектральный анализ заключается в разложении исходной функции на заданном интервале с помощью ряда Фурье по тригонометрическим функциям. Совокупность коэффициентов разложения представляет собой спектр исходной функции.
В качестве исходной информации для спектрального анализа используется график какого-либо физического процесса, полученного в результате исследования ММС. Наиболее часто используются характеристики механических величин: смещения, скорости, ускорения, силы, момента, давления и т. п.; электрических величин: тока, напряжения, заряда, индукции и многих других величин.
График физического процесса будем называть исходной функцией. Результатом спектрального анализа является спектр одной из следующих основных характеристик физического процесса.
− Амплитуда.
− Среднее квадратическое значение (СКЗ).
− Дисперсия.
− Плотность распределения.
Спектральный анализ выполняется следующим образом.
С помощью быстрого преобразования Фурье (БПФ) исходная функция преобразуется в тригонометрический ряд, называемый также исходным разложением.
,где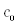 
, 
, 
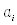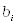– коэффициенты ряда Фурье; 
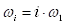– центр 
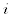-й частотной полосы исходного разложения, 
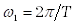– основная угловая частота; 
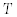– длина интервала разложения; 
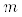– число частотных полос исходного разложения. Число частотных полос исходного разложения 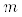зависит от 
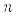– числа заданного количества точек исходной функции, используемых при быстром преобразовании Фурье: 
.
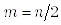, , – коэффициенты ряда Фурье; – центр -й частотной полосы исходного разложения, – основная угловая частота; – длина интервала разложения; – число частотных полос исходного разложения. Число частотных полос исходного разложения зависит от – числа заданного количества точек исходной функции, используемых при быстром преобразовании Фурье: .При необходимости пользователь может дополнить график интервалом с постоянным значением. В качестве постоянного значения используется среднее значение исходной функции на заданном интервале. Данная возможность может быть полезна для увеличения детализации спектра по частоте и смещения основной частоты в область низких частот. Стоит отметить, что абсолютные значения характеристик (например, амплитуды) при этом изменятся!
Обозначим за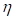 
частоту или угловую (круговую) частоту, в зависимости от выбора пользователя. Обозначим за 
(
) центр 
-й частотной полосы исходного разложения по частоте или угловой частоте, где 
, соответственно, основная частота 
или основная угловая частота .
частоту или угловую (круговую) частоту, в зависимости от выбора пользователя. Обозначим за 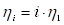(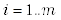) центр 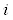-й частотной полосы исходного разложения по частоте или угловой частоте, где 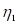, соответственно, основная частота 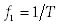или основная угловая частота 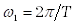.Через коэффициенты ряда Фурье определяются амплитуды и дисперсии для каждой частотной полосы исходного разложения. Амплитуда исходного разложения вычисляется по формуле
.Остальные параметры исходного разложения вычисляются по формулам
дисперсия:
;плотность распределения:
;среднее квадратическое значение:
.Отметим, что амплитуда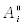 
, дисперсия 
и среднее квадратическое значение 
являются характеристиками полосы спектра, то есть дискретными величинами. В то время как плотность распределения представляется в виде непрерывной функции по частоте 
(рис.45).
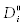, дисперсия и среднее квадратическое значение 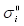являются характеристиками полосы спектра, то есть дискретными величинами. В то время как плотность распределения представляется в виде непрерывной функции по частоте 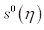(рис.45).
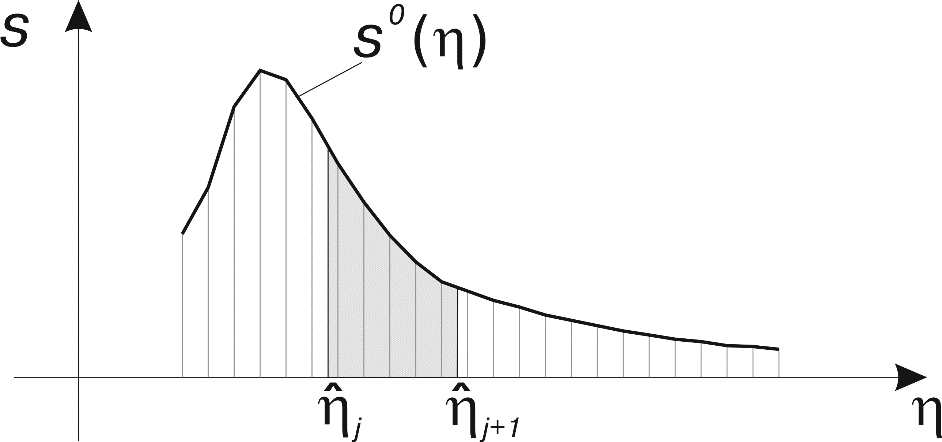
Рис. 45. Функция исходной плотности распределения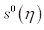
В качестве шкалы спектра по умолчанию используется исходное равномерное разбиение БПФ: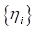 
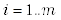, . Если пользователь указал шкалу спектра, отличную от шкалы по умолчанию, то по исходному спектру дисперсий и заданной пользовательской шкале спектра 
, 
, определяются основные характеристики спектра для каждой частотной полосы пользовательского спектра. Здесь – границы спектральных полос.
, . Если пользователь указал шкалу спектра, отличную от шкалы по умолчанию, то по исходному спектру дисперсий и заданной пользовательской шкале спектра 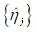, , 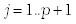определяются основные характеристики спектра для каждой частотной полосы пользовательского спектра. Здесь 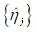– границы спектральных полос.Плотность распределения пользовательского спектра вычисляется по формуле
,где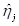 
, 
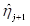– границы j-й частотной полосы пользовательского спектра.
, – границы j-й частотной полосы пользовательского спектра.Остальные параметры пользовательского спектра вычисляются по формулам
дисперсия:
;амплитуда:
;среднее квадратическое значение
.На точность вычисляемого процесса и полученного спектра, влияют следующие параметры.
− Параметры интегрирования при определении исходной функции.
− Шаг вывода результатов.
− Прореживание значений датчика при выводе на график.
− Заданное количество точек, используемых для равномерного представления исходной функции на выбранном интервале. Функция с равномерным распределением точек – это необходимое условие для выполнения быстрого преобразования Фурье.
Чтобы получить спектр для периодической функции с наименьшей погрешностью, необходимо задать интервал исходной функции с целым числом периодов.
При графическом отображении спектр может принимать следующий вид.
− Полосы. Спектр отображается в виде вертикальных полос для заданной частотной шкалы спектра.
− Огибающая. Спектр отображается в виде сплошной линии для заданной частотной шкалы спектра. Значение характеристики откладывается в центре частотной полосы (среднее арифметическое от ее границ).
− Линии. Спектр отображается в виде вертикальных линий для заданной частотной шкалы спектра. Линии находятся в центре частотных полос.
Применение спектрального анализа
К графику физического процесса можно применить спектральный анализ. Для этого необходимо выбрать команду Графики датчиков / Спектральный анализ / Настройка спектрального анализа. На экране появится окно Настройка спектрального анализа. Внешний вид этого окна представлен на Рис. 46. После осуществления всех настроек и их подтверждения откроется окно Спектральные характеристики с графическим отображением спектров. Это окно относится к окнам типа Графики датчиков, и для него доступны все аналогичные возможности.
Рассмотрим структуру окна Настройка спектрального анализа и назначение его элементов управления.
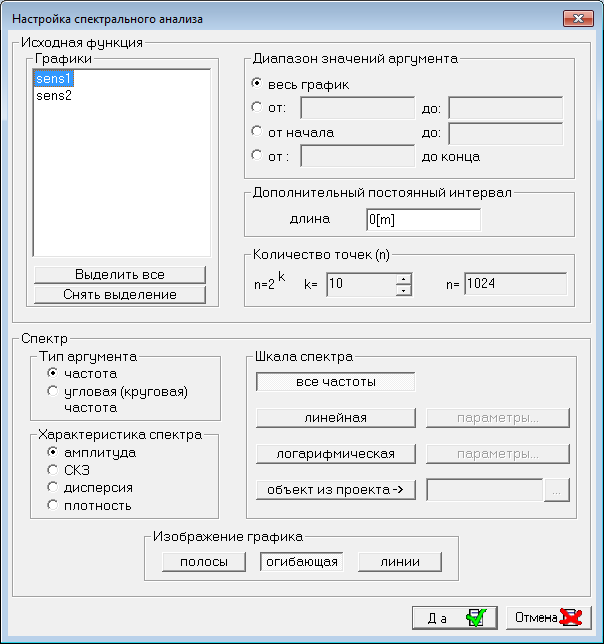
Рис. 46. Окно Настройка спектрального анализа
Область Исходная функция:
− Раздел Графики содержит список имен графиков, имеющихся в текущем окне графиков датчиков. Кнопки Выделить все и Снять выделение позволяют управлять выбором графиков датчиков, для которых применять спектральный анализ.
− Раздел Диапазон значений аргумента содержит настройки интервала исходных графиков. К выбранным графикам на этом интервале будет применено быстрое преобразование Фурье. В качестве единиц измерения по умолчанию используются установленные в свойствах проекта единицы, соответствующие размерности аргумента графика датчика.
− Раздел Дополнительный постоянный интервал определяет длину дополнительного интервала, на котором график дополняется постоянным значением. В качестве постоянного значения используется среднее значение для диапазона, заданного в разделе Диапазон значений аргумента. По умолчанию длина принимается равной нулю. В качестве единиц измерения по умолчанию используются установленные в свойствах проекта единицы, соответствующие размерности аргумента графика датчика.
− Раздел Количество точек (n) позволяет выбрать количество точек, используемое для равномерного представления исходной функции на заданном интервале при применении быстрого преобразования Фурье.
Область Спектр:
− Раздел Тип аргумента позволяет выбрать тип аргумента спектра («частота» / «угловая (круговая) частота»). По умолчанию используется «частота».
− Раздел Шкала спектра позволяет управлять настройками шкалы спектра. Пользователь может использовать шкалу по умолчанию («все частоты»), представляющую собой исходное равномерное разбиение БПФ, или задать линейную или логарифмическую шкалу, или воспользоваться объектами типа шкала спектра для просмотра спектра в заданном диапазоне частот.
− Раздел Характеристика спектра позволяет выбрать характеристику, для которой будет построен спектр («амплитуда» / «СКЗ» / «дисперсия» / «плотность»). По умолчанию используется «СКЗ».
− Раздел Изображение графика позволяет выбрать вид графического отображения спектра («полоса» / «огибающая» / «линии»). По умолчанию используется «полоса».
Для изменения настроек графического отображения спектра используется окно Редактирование спектра; окно открывается из контекстного меню графика спектра по команде Графики датчиков / Спектральный анализ / Редактирование спектра. Внешний вид этого окна представлен на Рис. 47. Это окно содержит те же настройки, что находятся в области Спектр окна Настройка спектрального анализа.
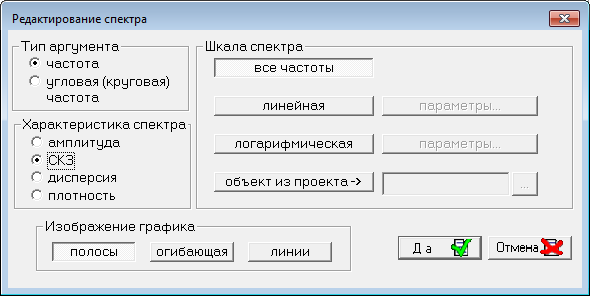
Рис. 47. Окно Редактирование спектра