7.8.3 Расчет реакций опорной поверхности в плоскости контакта
Расчет реакций опорной поверхности в плоскости контакта может производиться по общему, упрощенному или по смешанному алгоритму. В случае невыполнения гипотезы квазистационарности качения, например, при его отсутствии расчет осуществляется по упрощенному алгоритму.
Определение текущего расчетного случая осуществляется на основе анализа значения коэффициента продольного проскальзывания.
Если  , то расчет производится только по общему алгоритму.
, то расчет производится только по общему алгоритму.
Если  , то расчет реакций производится только по упрощенному алгоритму.
, то расчет реакций производится только по упрощенному алгоритму.
Иначе при  расчет производится по смешанному алгоритму, в котором
расчет производится по смешанному алгоритму, в котором
где  ,
,  – сила и стабилизирующий момент, рассчитанные по общему алгоритму;
– сила и стабилизирующий момент, рассчитанные по общему алгоритму;
 .
.В модели принято  ,
,  .
.
Расчет сил и моментов на эквивалентной плоскости при отсутствии качения
При отсутствии качения в касательной плоскости контакта используется линейная щеточная модель со следующими допущениями:
− пятно контакта сводится к одной точке, совпадающей с центром пятна контакта;
− в данной точке реализована модель «щетки»;
− жесткость щетки, включает в себя жесткость протектора, кольца и обода, соответствует, размещенной на пятне контакта;
− щетка имеет жесткость на кручение, реализуя тем самым действие стабилизирующего момента  .
.
Расчет продольной и боковой удельных жесткостей щетки сводится к расчету удельной эквивалентной жесткости щетки контакта, которая вычисляется по формуле:
При этом коэффициент эквивалентной жесткости
где  – площадь пятна контакта.
– площадь пятна контакта.
Угловая жесткость протектора вычисляется по формуле:
где  – угловое смещение щетки контакта;
– угловое смещение щетки контакта;  – поворачивающий момент щетки контакта, действующий вокруг оси
– поворачивающий момент щетки контакта, действующий вокруг оси  . При расчете угловой жесткости предполагается, что пятном контакта является круг.
. При расчете угловой жесткости предполагается, что пятном контакта является круг.
Угловая жесткость щетки  при этом складывается из жесткости протектора
при этом складывается из жесткости протектора  и жесткости углового смещения кольца относительно обода
и жесткости углового смещения кольца относительно обода  :
:
Для оценки силы трения в контакте между колесом и дорогой в каждый момент времени должны быть определены следующие параметры:
ось  ;
;
ось  ;
;
Здесь флаги  и
и  могут принимать следующие значения:
могут принимать следующие значения:
где  – контакта между концом щетки и эквивалентной плоскостью контакта на текущем шаге расчета нет;
– контакта между концом щетки и эквивалентной плоскостью контакта на текущем шаге расчета нет;  – контакт между концом щетки и эквивалентной плоскостью контакта на текущем шаге расчета есть;
– контакт между концом щетки и эквивалентной плоскостью контакта на текущем шаге расчета есть;
 ,
,где  – контакта между концом щетки и эквивалентной плоскостью контакта на предыдущем шаге расчета нет;
– контакта между концом щетки и эквивалентной плоскостью контакта на предыдущем шаге расчета нет;  – предполагается, что на предыдущем шаге расчета конец щетки фиксируется на эквивалентной плоскости контакта;
– предполагается, что на предыдущем шаге расчета конец щетки фиксируется на эквивалентной плоскости контакта; – предполагается, что на предыдущем шаге расчета конец щетки проскальзывает по эквивалентной плоскости контакта.
– предполагается, что на предыдущем шаге расчета конец щетки проскальзывает по эквивалентной плоскости контакта.
Расчет силы трения и стабилизирующего момента производится в следующей последовательности:
Если  , то
, то  .
.  . Завершение расчетного шага.
. Завершение расчетного шага.
Если  и
и  , то
, то  ,
,  . Завершение расчетного шага.
. Завершение расчетного шага.
Расчет деформации щетки в проекциях на оси  ,
, и угловой деформации на ось
и угловой деформации на ось  на текущем шаге с учетом наличия контакта на предыдущем шаге расчета по формулам:
на текущем шаге с учетом наличия контакта на предыдущем шаге расчета по формулам:
где  ,
,  ,
,  ,
,  – проекции скорости скольжения щетки контакта на оси X и Y соответственно на текущем и прошлом шагах соответственно;
– проекции скорости скольжения щетки контакта на оси X и Y соответственно на текущем и прошлом шагах соответственно; ,
,  – проекции угловой скорости щетки контакта на ось Z на текущем и прошлом шагах соответственно;
– проекции угловой скорости щетки контакта на ось Z на текущем и прошлом шагах соответственно;  – значение времени на текущем шаге расчета. Построение вектора деформации щетки на текущем шаге
– значение времени на текущем шаге расчета. Построение вектора деформации щетки на текущем шаге  .
.
Если  , то предполагается что сила трения и ее момент по абсолютному значению ограничены величинами
, то предполагается что сила трения и ее момент по абсолютному значению ограничены величинами
где  – упругая компонента нормальной контактной силы;
– упругая компонента нормальной контактной силы;  – коэффициент трения скольжения в контакте;
– коэффициент трения скольжения в контакте;  – радиус кольца с эквивалентной кругу радиуса
– радиус кольца с эквивалентной кругу радиуса  угловой жесткостью (данное соотношение получено на основе верификации с экспериментальными данными).
угловой жесткостью (данное соотношение получено на основе верификации с экспериментальными данными).
Сила трения и ее момент определяется следующими выражениями с учетом ограничений
где  – проекция вектора деформации щетки на текущем шаге
– проекция вектора деформации щетки на текущем шаге  на эквивалентную плоскость;
на эквивалентную плоскость; 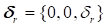 – вектор угловой деформации щетки на текущем шаге.
– вектор угловой деформации щетки на текущем шаге.
Завершение расчетного шага.
Если  , то предполагается что сила трения и ее момент
, то предполагается что сила трения и ее момент
Сила трения и ее момент по абсолютному значению рассчитывается с учетом ограничения по предельной величине
Завершение расчетного шага.
Параметры контакта при завершении расчетного шага интегрирования определяются следующим образом:
Если  , то
, то
Если  , то
, то
Если и
и  , то
, то
Если и
и  , то
, то
 .
.Если и
и  , то
, то
Расчет сил и моментов на эквивалентной плоскости при квазистационарном качении
Общий алгоритм расчета при квазистационарном качении описан в последующих пунктах, схема алгоритма приведена на рис.27.

Рис. 27. Структурная схема общего алгоритма расчета реакций в плоскости контакта
Геометрические характеристики пятна контакта
Иллюстрация к определению геометрических характеристик пятна контакта представлена на рис.28.
Расчетная плоскость протектора перпендикулярна оси вращения колеса и проходит через центр пятна контакта. В расчетах используется скорректированная форма пятна контакта. Коррекция пятна контакта для приближения к экспериментальным данным производится масштабированием по его продольной оси на коэффициент  .
.
Соответственно, характерная расчетная полудлина пятна контакта определяется следующим образом:
где  – исходная характерная полудлина пятна контакта,
– исходная характерная полудлина пятна контакта,  – корректировочный коэффициент, который уточняется по экспериментальным данным.
– корректировочный коэффициент, который уточняется по экспериментальным данным.
Радиус профиля недеформированной шины в расчетной плоскости протектора определяется по зависимости (24):
Расчетное значение радиуса профиля недеформированной шины определяется следующим образом:
 .
.Боковое отклонение нижней точки расчетной окружности протектора определяется по формуле:
где  – расстояние от центра контакта
– расстояние от центра контакта  до оси вращения колеса, определяемое соотношением:
до оси вращения колеса, определяемое соотношением:
Угол сектора расчетного пятна контакта определяется следующим образом:
 .
.Также в процессе расчета рассчитывается функция ширины скорректированного пятна контакта  в зависимости от продольной координаты пятна контакта.
в зависимости от продольной координаты пятна контакта.

Рис. 28. Геометрические характеристики пятна контакта
Распределение нормального давления в пятне контакта
В модели принято, что нормальное давление в пятне контакта постоянно по ширине пятна контакта, а по длине распределено кусочно-линейно, по трапеции, как это показано на рис.29.

Рис. 29. Распределение нормального давления в пятне контакта
Уравнение линии эпюры нормальных давлений по длине контакта описывается следующей зависимостью:

где  – координата точки пятна контакта вдоль продольной оси пятна контакта;
– координата точки пятна контакта вдоль продольной оси пятна контакта;
Коэффициенты  и
и  определяются из следующих соображений:
определяются из следующих соображений:
1) сумма элементарных нормальных сил по всей площади контакта равна нормальной реакции опорной плоскости с учетом демпфирования:
 ;
;2) сумма элементарных моментов относительно оси  по длине контакта равна моменту сопротивления качению (с точностью до знака):
по длине контакта равна моменту сопротивления качению (с точностью до знака):
 .
.Возможен случай такой совокупности значений  и
и  , что один из параметров
, что один из параметров  или
или  эпюры нормальных давлений будет отрицательным при расчете по приведенным выше формулам (красная линия на рис.30). Это считается недопустимым. В этом случае величина момента сопротивления качению
эпюры нормальных давлений будет отрицательным при расчете по приведенным выше формулам (красная линия на рис.30). Это считается недопустимым. В этом случае величина момента сопротивления качению  не выдерживается, трапеция вырождается в треугольник (синяя линия на рис.30). Таким образом, условие 2 в случае
не выдерживается, трапеция вырождается в треугольник (синяя линия на рис.30). Таким образом, условие 2 в случае  не выполняется; параметры эпюры вычисляются на основе условия 1.
не выполняется; параметры эпюры вычисляются на основе условия 1.

Рис. 30. Недопустимый случай распределения нормального давления
и его корректировка
Расчет характеристик элементов протектора в пятне контакта
Расчетная область пятна контакта разделяется на  элементов, как это показано на рис.31.
элементов, как это показано на рис.31.

Рис. 31. Разбиение пятна контакта
Линии раздела элементов перпендикулярны продольной оси пятна контакта. Длины всех элементов вдоль продольной оси одинаковы. Длина отдельного элемента равна:
В соответствии с полученной ранее зависимостью  для ширины пятна контакта определяются площади
для ширины пятна контакта определяются площади  (
( ) каждого элемента (
) каждого элемента ( – координата центра
– координата центра  -го элемента вдоль продольной оси пятна контакта).
-го элемента вдоль продольной оси пятна контакта).
 (
(Упругие свойства протектора определяются следующими параметрами:
−  – жесткость сдвига протектора в продольном направлении, приходящаяся на единицу площади пятна контакта;
– жесткость сдвига протектора в продольном направлении, приходящаяся на единицу площади пятна контакта;
−  – жесткость сдвига протектора в боковом направлении, приходящаяся на единицу площади пятна контакта.
– жесткость сдвига протектора в боковом направлении, приходящаяся на единицу площади пятна контакта.
Коэффициенты жесткости  -го элемента пятна контакта в продольном и боковом направлениях определяются следующим образом:
-го элемента пятна контакта в продольном и боковом направлениях определяются следующим образом:
Сила нормального давления  -го элемента на опорную плоскость вычисляется по формуле:
-го элемента на опорную плоскость вычисляется по формуле:
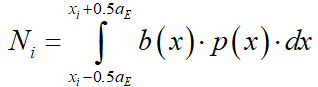 .
.Мгновенный центр поворота колеса на эквивалентной плоскости и скоростные характеристики контакта
Угловая скорость поворота колеса на эквивалентной плоскости определяется следующим образом:
Мгновенный центр поворота колеса находится на проходящем через центр колеса перпендикуляре к проекции линейной скорости колеса на опорную плоскость. Мгновенный центр поворота отстоит от центра колеса на расстояние  , определяемое из кинематических соотношений в соответствии с рис.32:
, определяемое из кинематических соотношений в соответствии с рис.32:
 .
.
Рис. 32. Мгновенный центр поворота колеса
Расчет деформаций элементов протектора в пятне контакта и реакций  ,
,  ,
,  опорной поверхности
опорной поверхности
В рассматриваемой модели расчет деформаций элементов пятна контакта производится в предположении стационарного качения колеса по эквивалентной плоскости. Строго говоря, гипотеза стационарности качения колеса означает выполнение следующих условий
В действительности достаточно, чтобы параметры  ,
,  ,
,  ,
,  ,
, 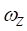 не имели существенных изменений за характерное время перемещения пятна контакта, равное
не имели существенных изменений за характерное время перемещения пятна контакта, равное  .
.
Для расчета деформаций элементов используется смещенное положение пятна контакта, которое возникает в результате отклонения АК от обода. При этом предполагается, что геометрические характеристики пятна контакта и распределение нормального давления в нем не изменились по сравнению с исходным положением.
Положение внутренних (связанных с АК) точек элементов контакта представлено на рис.33. Линия положения верхних точек описывается следующей функцией
 ,
,где параметр  определяет направление деформации элементов поперечного сектора шины относительно нормали к поверхности (см. пункт 7.5).
определяет направление деформации элементов поперечного сектора шины относительно нормали к поверхности (см. пункт 7.5).
Значение  влияет главным образом на значение боковой силы при прямолинейном качении колеса с наклоном. Значение
влияет главным образом на значение боковой силы при прямолинейном качении колеса с наклоном. Значение  выбирается из отрезка
выбирается из отрезка  . При
. При  боковая сила при прямолинейном качении колеса с наклоном будет отсутствовать, а при
боковая сила при прямолинейном качении колеса с наклоном будет отсутствовать, а при  она будет иметь максимальное значение. В модели принято
она будет иметь максимальное значение. В модели принято  .
.

Рис. 33. Положение внутренних (связанных с АК) точек элементов контакта
Положение внешних (контактирующих с опорной поверхностью) точек элементов контакта определяется из условий их неподвижности на опорной плоскости, обеспечиваемой силами трения, и проскальзывания в том случае, если сила трения превышает трение покоя. Расчет начинается с набегающего при качении элемента и от него продолжается последовательно по всем элементам. Набегающим является первый или последний элемент пятна контакта. Для удобства изложения алгоритма будем считать, что набегающим является первый элемент. В этом случае расчет положения нижних точек, деформаций элементов пятна контакта и сил, действующих на них, производится по следующему алгоритму.

где  – скорость перемещения
– скорость перемещения  -й нижней точки в системе координат пятна контакта;
-й нижней точки в системе координат пятна контакта;
По предварительным векторам деформаций  для каждого элемента контакта определяются окончательные вектора деформаций
для каждого элемента контакта определяются окончательные вектора деформаций 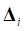 и окончательные вектора сил
и окончательные вектора сил  по алгоритму, приведенному в пункте 7.7. При этом в качестве жесткостей
по алгоритму, приведенному в пункте 7.7. При этом в качестве жесткостей  и
и  используются продольная и поперечная жесткости
используются продольная и поперечная жесткости  -го элемента контакта
-го элемента контакта  и
и  , а в качестве радиальной деформации
, а в качестве радиальной деформации  используется сила нормального давления на
используется сила нормального давления на  -й элемент контакта
-й элемент контакта  . Сила
. Сила  действует на
действует на  -й элемент контакта в эквивалентной плоскости и приложена в точке
-й элемент контакта в эквивалентной плоскости и приложена в точке  . Окончательное положение соскользнувшей нижней точки
. Окончательное положение соскользнувшей нижней точки  определяется соотношением
определяется соотношением  .
.
Графическая иллюстрация алгоритма расчета положения нижних точек и деформаций элементов пятна контакта представлена на рис.34.
Реакции опорной поверхности в системе координат  и их момент относительно центра
и их момент относительно центра  определяются следующим образом:
определяются следующим образом:
где  – координаты верхней точки
– координаты верхней точки  -го элемента контакта
-го элемента контакта  .
.

Рис. 34. Расчет деформаций элементов протектора в пятне контакта
Расчет поворота безмассового кольца брекера относительно обода
Предполагается, что кольцо брекера поворачивается относительно обода под действием стабилизирующего момента.
Вектор поворота кольца вокруг своего центра (вектор приведенных параметров Эйлера) определяется следующим образом:
где  – проекция стабилизирующего момента на эквивалентную плоскость;
– проекция стабилизирующего момента на эквивалентную плоскость;