1.2.21 Функция гармонических колебаний с переменной частотой
Данный метод создает не одну функцию, а массив функций. Поэтому тип объекта, создаваемого этим методом, записывается в файле проекта не function, а function_array.Данный метод создает функцию гармонических колебаний по времени с переменной частотой. Функция имеет один аргумент – время. График создаваемой функции представлен на рис. 4. Дополнительно создается график зависимость частоты колебаний от времени, он представляет собой ступенчатую функцию. Вид функции изображен на рис. 5.
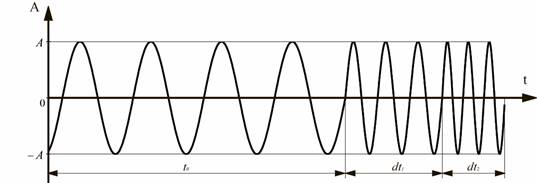
Рис. 4. Функция гармонических колебаний с переменной частотой
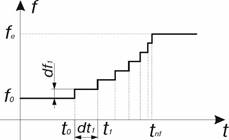
Рис. 5. Функция изменения частоты гармонических колебаний
Синтаксис метода создания
varFreq( A, t0, n, f0, fe, nf, freqChange= , Harmonic = )
Обязательные позиционные параметры метода
scalar A
Амплитуда колебаний.
scalar f0
Начальная частота колебаний.
scalar fe
Конечная частота колебаний.
scalar t0
Время начала изменения частоты.
scalar n
Количество периодов колебаний на переходных участках постоянной частоты.
scalar nf
Количество переходных участков постоянной частоты.
Необязательные именованные параметры метода
freqChange = [relative:/absolute:]
Тип изменения значения частоты между участками. По умолчанию используется относительное изменение частоты freqChange = relative:.
freqChange = relative:Относительное изменение значения частоты между участками. Значения частот на участках в этом случае представляют собой геометрическую прогрессию.
freqChange = absolute:Абсолютное изменение значения частоты между участками. Значения частот на участках в этом случае представляют собой арифметическую прогрессию.
Harmonic = [cos:/sin:]
Вид гармонической функции. По умолчанию Harmonic = cos:.
Harmonic = cos:Гармоническая функция – косинусоида.
Harmonic = sin:Гармоническая функция – синусоида.
Описание
До момента времени t0 частота гармонических колебаний равна f0.
В момент времени t0 происходит первое изменение частоты на величину df, она зависит от количества участков постоянной частоты n, начальной и конечной частоты колебаний f0 и fe, а также от параметра freqChange.
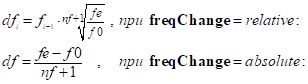
После того, как частота примет конечное значения fe, колебания будут продолжаться на этой частоте.
Таким образом создается ступенчатая функция зависимости частоты гармонических колебаний от времени. График функции изображен на рис. 5.
Функция колебаний состоит из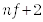 
участка, на которых амплитуда колебаний одинакова, но частота различается. Размерность амплитуды колебаний может быть любой. На рис. 4 изображен график этой функции.
участка, на которых амплитуда колебаний одинакова, но частота различается. Размерность амплитуды колебаний может быть любой. На рис. 4 изображен график этой функции.Колебания на каждом i-м участке являются гармоническими и задаются функцией:
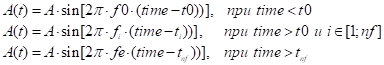
где функция гармонических колебаний может быть, как синус, так и косинус, в зависимости от параметра Harmonic;
частота колебаний на i-м участке определяются по формуле: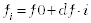 
;
;длительность каждого участка с постоянной частотой определяется по формуле: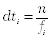 
;
;момент времени начала i-го участка определяется так: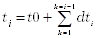 
.
.