3.1 Стабилизация груза

В примере рассматривается стабилизация груза в требуемом положении. В начальный момент времени груз находится в состоянии покоя на заданном расстоянии от требуемого положения. К центру масс груза прикладывается управляющая сила, которая перемещает груз в требуемое положение.

Схема рассматриваемой системы показана на рис. 1.

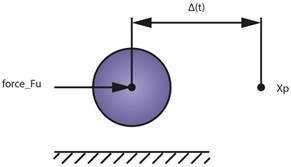
Рис. 1. Схема стабилизации положения груза

Стабилизация положения груза осуществляется управляющей силой. Для управления используется классический регулятор следующего вида:

где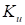

– коэффициент управляющей силы,

– параметр управления;

– рассогласование по положению;

– производная рассогласования;

– коэффициенты регулятора.

Исходные данные для расчета:

− масса груза 1 [kg],

− радиус груза 0.1 [m],

− коэффициент управляющей силы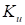

1 [N],

− требуемое положение груза 1 [m],

− период обновления сигнала системы управления 0.001 [s],

− коэффициент усиления системы управления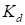

-30 [s/m],

− коэффициент усиления системы управления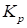

-1000 [1/m].

Моделирование управляющей силы может производиться как непосредственно в проекте EULER, так и в отдельной модели, созданной в MATLAB/Simulink и включенной в проект EULER.

Файл stabG_EULER.elr содержит модель стабилизации груза. Моделирование управляющей силы выполняется непосредственно в ПК EULER (текст файла приведен ниже).

Текст проекта stabG_EULER.elr

// Стабилизация положения груза в заданной точке.

// Датчик сигнала управления

sensor signal "сигнал управления"=var( 0 );

// Инерциальное звено

color color_base=index( 5 );

body base=body( color = color_base );

set ground = base;

// Управляемый груз

scalar mG "масса груза"=1 [kg];

scalar Ku "коэффициент управляющей силы"=1 [N];

point point1=point( 0 [ m ], 0 [ m ], 0 [ m ] );

solid solid1=sphere( point1, 0.1 [ m ], mass = mG );

color color_G=index( 63 );

body G=body( color = color_G );

body G < ( solid1 );

joint joint1=translational( base, G, point1, projectX );

sensor Fu "значение управляющей силы"=signal*Ku;

force force_Fu "управляющая сила"=force( G, point1, projectX, Fu, list( ) );

sensor X "положение груза"=joint1.s;

sensor Xt "скорость груза"=derivative( X );

// Система управления

scalar XP "требуемое положение груза"=1 [m];

// параметры рассогласования

sensor d "рассогласование"=X-XP;

sensor dt "производная рассогласования"=Xt;

// алгоритм управления

scalar Kd=-30 [s/m];

scalar Kp=-1000 [1/m];

sensor signal_1=Kd*dt+Kp*d;

// Переопределение сигнала управления

sensor signal_2=currentValue( signal, signal_1 );

command dynam_RK4_p001 "команда расчета движения"=constRK4( 1.00000e+000 [ s ], 1.00000e-003 [ s ] );

/\///////////////////////////////////////////////////////////////////////////////////

/\ Список главных команд;

set dynamics = dynam_RK4_p001;

/\///////////////////////////////////////////////////////////////////////////////////

/\ Единицы измерения;

set units = SI;

Файл stabG_EULER_Simulink.elr (текст файла приведен ниже) содержит модель стабилизации груза с моделированием управляющей силы в DLL-модуле, который создан в MATLAB/Simulink. Входными данными этого модуля управления являются данные о движении груза (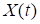

– координата груза и

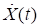– производная координаты груза). В соответствии с представленным алгоритмом в модуле формируется сигнал управления и его значение в виде выходного параметра возвращается в общую модель стабилизации груза (в ПК EULER). Схема (алгоритм расчета) модуля управления в программном комплексе MATLAB/Simulink представлена на рис. 2.

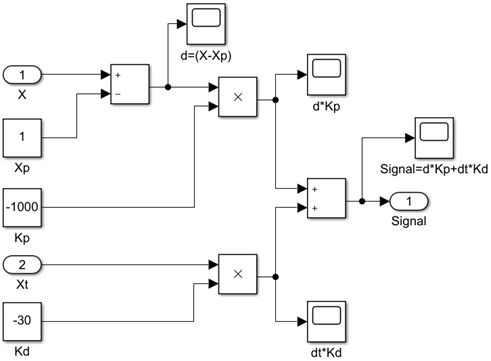
Рис. 2. Схема управляющего модуля в программном комплексе MATLAB/Simulink

Текст проекта stabG_EULER_Simulink.elr

// Стабилизация положения груза в заданной точке.

// Датчик сигнала управления

sensor signal "сигнал управления"=var( 0 );

// Инерциальное звено

color color_base=index( 5 );

body base=body( color = color_base );

set ground = base;

// Управляемый груз

scalar mG "масса груза"=1 [kg];

scalar Ku "коэффициент управляющей силы"=1 [N];

point point1=point( 0 [ m ], 0 [ m ], 0 [ m ] );

solid solid1=sphere( point1, 0.1 [ m ], mass = mG );

color color_G=index( 63 );

body G=body( color = color_G );

body G < ( solid1 );

joint joint1=translational( base, G, point1, projectX );

sensor Fu "значение управляющей силы"=signal*Ku;

force force_Fu "управляющая сила"=force( G, point1, projectX, Fu, list( ) );

sensor X "положение груза"=joint1.s;

sensor Xt "скорость груза"=derivative( X );

// Система управления

scalar step=1.00000e-04 [ s ];

string U="X [ m ],Xt [ m / s ]";

string Y="signal [ ]";

sensor_array DLL=simulink("gruz.dll", U, Y, "", step);

// Переопределение сигнала управления

sensor signal_2=currentValue( signal, DLL.signal );

command dynam_RK4_p001 "команда расчета движения"=constRK4( 1.00000e+000 [ s ], 1.00000e-003 [ s ] );

/\///////////////////////////////////////////////////////////////////////////////////

/\ Список главных команд;

set dynamics = dynam_RK4_p001;

/\///////////////////////////////////////////////////////////////////////////////////

/\ Единицы измерения;

set units = SI;

В результате расчета стабилизации положения груза при помощи моделей stabG_EULER.elr и stabG_EULER_Simulink.elr получены совпадающие результаты.

На рис. 3 и рис. 4 представлены графики управляющей силы и положения груза, полученные при расчете модели stabG_EULER.elr, на рис. 5 – совпадающие графики положения груза, полученные при расчете моделей stabG_EULER.elr и stabG_EULER_Simulink.elr.

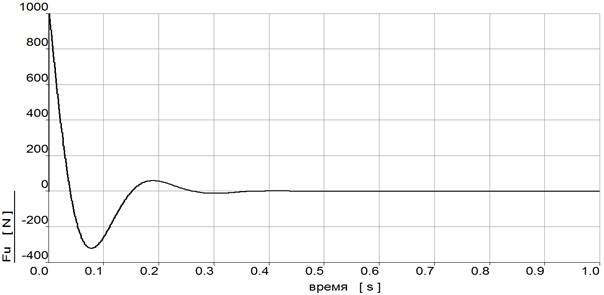
Рис. 3. Управляющая сила

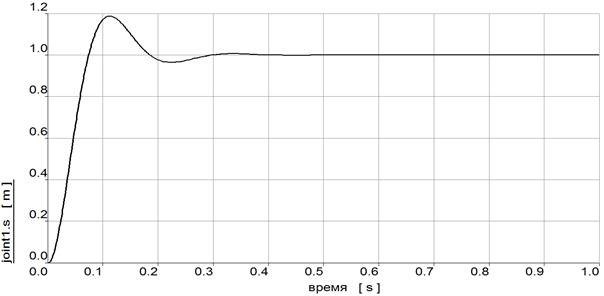
Рис. 4. Положение груза, рассчитанное в модели stabG_EULER.elr

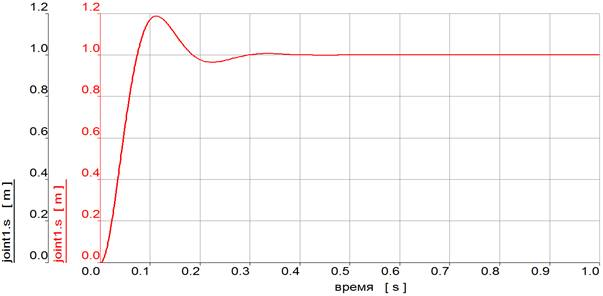
Рис. 5. Совпадающие результаты расчета положения груза в моделях stabG_EULER_Simulink.elr и stabG_EULER.elr