2.3 Струя реактивного двигателя
 Среда описывает скорость, плотность и температуру струи реактивного двигателя. Сам двигатель может перемещаться в пространстве, но предполагается, что окружающая его среда неподвижна в инерциальном пространстве. Струя является осесимметричной. Вектор скорости струи не изменяет своего направления относительно системы координат связанной с соплом. В качестве исходных параметров задаются: радиус сопла реактивного двигателя, скорость струи на срезе сопла, температура струи на срезе сопла, молекулярная масса газа в реактивной струе, удельная теплоемкость газа в реактивной струе. В качестве необязательных параметров среды могут быть заданы: давление, температура, плотность и молекулярная масса окружающей среды.
Среда описывает скорость, плотность и температуру струи реактивного двигателя. Сам двигатель может перемещаться в пространстве, но предполагается, что окружающая его среда неподвижна в инерциальном пространстве. Струя является осесимметричной. Вектор скорости струи не изменяет своего направления относительно системы координат связанной с соплом. В качестве исходных параметров задаются: радиус сопла реактивного двигателя, скорость струи на срезе сопла, температура струи на срезе сопла, молекулярная масса газа в реактивной струе, удельная теплоемкость газа в реактивной струе. В качестве необязательных параметров среды могут быть заданы: давление, температура, плотность и молекулярная масса окружающей среды.Важно отметить, что данная среда предназначена только для моделирования силовых воздействий на элементы стационарных стартовых сооружений включая объекты их окружения.
|
Синтаксис метода создания
mediumJet(BaseNode,r0, u0, T0, mu, c_p, pressure_env=…, temperature_env=…, mu_nenv=…, rho_env=….)
Обязательные позиционные параметры метода
node BaseNode
Узел принадлежащий соплу двигателя. Ось X должна быть направлена по истечению среды.
scalar r0 [length]
Радиус среза сопла.
scalar u0 [length/time]
Скорость струи на срезе сопла.
scalar T0 [temperature]
Температура струи на срезе сопла.
scalar mu []
Молекулярная масса газа в струе.
scalar c_p [energy/mass /temperature]
Удельная теплоемкость газа в струе.
Необязательные именованные параметры метода
 pressure_env = scalar [pressure]
pressure_env = scalar [pressure]Давление окружающей среды. По умолчанию считается равным атмосферному давлению при нормальных условиях*, а именно 101,325 [kPa].
 temperature_env= scalar [temperature]
temperature_env= scalar [temperature]Температура окружающей среды. По умолчанию считается равной температуре при нормальных условиях*, а именно 293,15 [K].
 mu_env = scalar []
mu_env = scalar []Молекулярная масса газа в окружающей среде. По умолчанию принято стандартное значение для сухого воздуха равное 29,97.
 rho_env = scalar [mass/length3]
rho_env = scalar [mass/length3]Плотность газа окружающей среды. По умолчанию считается равной плотности воздуха при нормальных условиях*, а именно 1,225 [kg/m3].
*Нормальные условия согласно ГОСТ 2939-63 «Газы. Условия для определения объема».
Внутренние системные объекты
scalar P [N]
Тяга двигателя по заданным данным.
Описание
Поток газа из сопла реактивного двигателя представляет собой турбулентную струю, границу которой составляют поверхности тангенциального разрыва. Разрыв терпят такие параметры, как скорость течения, температура и другие, при этом распределение статического давления, то есть давления покоящего газа, создаваемого силой тяжести, оказывается непрерывным. При истечении сверхзвуковой струи из сопла на расчётном режиме, то есть с оптимальным режимом расширения сопла, статическое давление в струе не отличается от давления окружающей среды.
Для расчётов приняты следующие допущения:
Истечение из сопла происходит на расчётном режиме. Таким образом давление в струе на срезе сопла равно давлению окружающей среды.
1. Профили скорости и температуры на срезе сопла являются равномерными (значения скорости и температуры одинаковы в каждой точке на срезе сопла).
2. В струе отсутствует горение после выхода из сопла.
3. Скорость движения окружающей среды относительно струи значительно меньше, то есть струя считается затопленной.
4. Ввиду трудоёмкости расчёта с учётом сжимаемости, рассматривается струя несжимаемой жидкости.
5. Сопло имеет осесимметричную форму
Определение скорости струи в любой точке пространства
При истечении в однородную среду свободная затопленная турбулентная струя постепенно расширяется и рассеивается (рис. 1).
Для определения параметров струи необходимо рассчитать распределения скорости и температуры вдоль оси струи. При этом, эксперименты со струями при сверхзвуковых скоростях и высоких температурах показали, что профили скорости и температуры газа не деформированы по сравнению с соответствующими профилями в несжимаемой жидкости. Таким образом, при расчётах используются выражения для струй несжимаемой жидкости.
На начальном участке течения вблизи оси струя имеет выраженное ядро, относительная скорость потока в котором остается постоянной и равняется скорости на срезе сопла 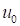 . Вдоль оси струи ядро постепенно уменьшается в радиальном направлении и к концу начального участка полностью исчезает. В радиальном направлении скорость уменьшается при удалении от оси и на границе достигает нуля.
. Вдоль оси струи ядро постепенно уменьшается в радиальном направлении и к концу начального участка полностью исчезает. В радиальном направлении скорость уменьшается при удалении от оси и на границе достигает нуля.
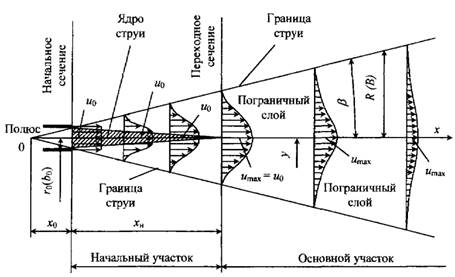
Рис. 1. Схема движения свободной затопленной турбулентной струи.
В принятой схеме расчёта в переходном сечении граница струи претерпевает излом. В действительности угол наклона границ плавно изменяется на протяжении переходного участка. Однако в упрощённых схемах расчёта принимают длину переходного участка равной нулю, а переходное сечение помещают в начало основного участка.
Тогда длина объединенного начального и переходного участка будет равна:
где 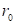 – радиус сопла.
– радиус сопла.
В случае пренебрежения переходным участком, угол наклона прямых границы ядра 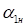 , соединяющих срез сопла и центр переходного сечения, и угол наклона прямых внешней границы струи
, соединяющих срез сопла и центр переходного сечения, и угол наклона прямых внешней границы струи 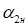 к оси будут равны в зависимости от радиуса струи
к оси будут равны в зависимости от радиуса струи 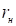 в переходном сечении:
в переходном сечении:
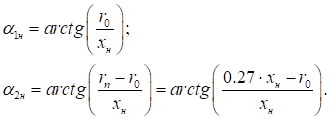
Профиль скорости вне ядра в произвольной точке сечения начального участка струи определяется безразмерной координатой 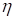 , отсчитываемой от внешней границы струи:
, отсчитываемой от внешней границы струи:
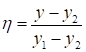 ,
, где 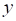 – расстояние от оси струи до произвольной точки сечения;
– расстояние от оси струи до произвольной точки сечения;
Осредненные скорости в произвольных точках сечения струи в пределах начального участка можно определить по следующей формуле Шлихтинга:
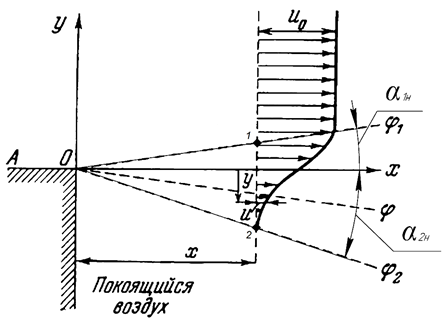
Рис. 2. Схема пограничного слоя затопленной струи.
Часть струи, расположенная за переходным сечением, называется основным участком. Угол между осью струи и внешней границей на данном участке равен:
На основном участке скорость на оси 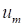 по мере удаления от сопла постепенно уменьшается. Скорость на оси
по мере удаления от сопла постепенно уменьшается. Скорость на оси 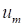 относительно расстояния от сопла
относительно расстояния от сопла 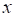 определяется формулой:
определяется формулой:
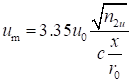 ,
, где 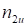 – коэффициент, учитывающий неравномерность полей скорости и плотности на срезе сопла,
– коэффициент, учитывающий неравномерность полей скорости и плотности на срезе сопла, 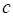 – опытный коэффициент, для начального участка струи равный 0.27.
– опытный коэффициент, для начального участка струи равный 0.27.
Так как принято допущение о равномерности профилей скорости и плотности на срезе сопла, 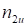 = 1. Тогда (4) принимает вид:
= 1. Тогда (4) принимает вид:
Распределение скоростей в радиальном направлении имеет подобные профили и определяется в зависимости от безразмерной координаты, отсчитываемой от оси струи:
где 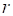 – радиус сечения струи.
– радиус сечения струи.
Профиль скорости в произвольном сечении на основном участке определяется следующей формулой Шлихтинга:
Скорость в любой точке пространства определяется по формуле (7). Произвольная точка принадлежит единственному поперечному сечению, осевая скорость 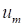 которого уже известна.
которого уже известна.
Определение температуры и плотности в струе
Температура на оси струи 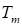 связана со скоростью следующим выражением:
связана со скоростью следующим выражением:
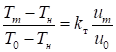 ,
, где 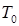 – температура на срезе сопла;
– температура на срезе сопла;
Коэффициент 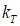 из выражения (8), для осесимметричной струи определяется формулой. В случае пренебрежения переходным участком, этот коэффициент равен:
из выражения (8), для осесимметричной струи определяется формулой. В случае пренебрежения переходным участком, этот коэффициент равен: 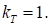
Профиль температуры торможения для струй большой скорости в произвольном сечении имеет универсальный характер, то есть является подобным при любых параметрах истечения и геометрии сопла.
Температура торможения равна:
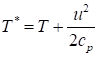 ,
, где 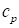 – удельная теплоёмкость рассматриваемого газа при постоянном давлении.
– удельная теплоёмкость рассматриваемого газа при постоянном давлении.
Профиль температуры торможения 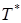 в произвольном сечении начального и основного участка в зависимости от безразмерных координат (2) и (6) соответственно можно определить по формулам:
в произвольном сечении начального и основного участка в зависимости от безразмерных координат (2) и (6) соответственно можно определить по формулам:
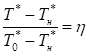 ;
; 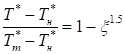 .
. Температура торможения окружающей среды 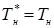 , так как скорость окружающей среды принята равной нулю.
, так как скорость окружающей среды принята равной нулю.
Так как считается, что истечение сверхзвуковой струи происходит на расчётном режиме, то статическое давление в струе и в окружающей среде одинаково. Тогда по уравнению Менделеева-Клайперона плотность в произвольной точке струи равна:
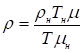 ,
, где 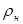 – плотность окружающего воздуха;
– плотность окружающего воздуха;
Также можно определить тягу двигателя по известным данным, воспользовавшись следующей формулой:
где 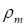 – плотность газа на срезе сопла;
– плотность газа на срезе сопла;
Для определения плотности газа на срезе сопла воспользуемся уравнением состояния идеального газа:
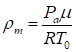 , (15)
, (15)где 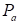 – атмосферное давление;
– атмосферное давление;