2.2.19 Случайная функция, задаваемая спектром
 Данный метод создает случайную функцию на заданном интервале. Функция имеет один аргумент.
Данный метод создает случайную функцию на заданном интервале. Функция имеет один аргумент.Функция определяется только на заданном интервале по аргументу; это используется для ускорения расчета. За пределами этого интервала функция полагается равной нулю. Математическое ожидание случайной функции равно нулю.
Флаг frequency:/angularFrequency: определяет как будут интерпретироваться значения заданной пользователем шкалы спектра: как частота 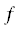 или угловая (круговая) частота
или угловая (круговая) частота 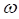 (общее обозначение, используемое далее –
(общее обозначение, используемое далее – 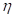 ). Под частотой понимается величина, обобщенная на случай произвольной размерности аргумента функции (см. раздел «Шкала спектра (spectralScale)» главы «Служебные объекты»).
). Под частотой понимается величина, обобщенная на случай произвольной размерности аргумента функции (см. раздел «Шкала спектра (spectralScale)» главы «Служебные объекты»).
Для размерности физической величины будем использовать обозначение 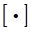 . Так
. Так 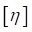 – размерность шкалы спектра,
– размерность шкалы спектра, 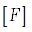 – размерность случайной функции,
– размерность случайной функции,  – размерность аргумента функции. Размерность аргумента функции зависит от того, как интерпретируются значения шкалы спектра:
– размерность аргумента функции. Размерность аргумента функции зависит от того, как интерпретируются значения шкалы спектра: 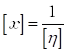 , если
, если  , и
, и 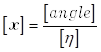 , если
, если 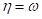 .
.
Синтаксис метода создания
random1(Frequency, SpectralScale, Distribution, DistributionFunction, x0, deltax, randomDetail=…, randomType=…)
Обязательные позиционные параметры метода
Frequency = [frequency:/angularFrequency:]
Параметр определяет тип аргумента для функции распределения.
 Frequency = frequency:
Frequency = frequency:Частота.
 Frequency = angularFrequency:
Frequency = angularFrequency:Угловая частота.
spectralScale SpectralScale
Шкала спектра.
Distribution = [amplitude:/density:/dispersion:/rootMeanSquare:]
Параметр определят тип функции распределения
 Distribution = amplitude:
Distribution = amplitude:Функция распределения амплитуды по полосам шкалы спектра 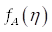 . Размерность совпадает с размерностью случайной функции:
. Размерность совпадает с размерностью случайной функции: 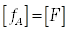 .
.
 Distribution = density:
Distribution = density:Плотность распределения дисперсии по частоте. Размерность представляет собой квадрат размерности случайной функции, деленной на размерность частоты или угловой частоты: 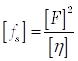 .
.
 Distribution = dispersion:
Distribution = dispersion:Функция распределения дисперсии по полосам шкалы спектра 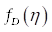 . Размерность представляет собой квадрат размерности случайной функции:
. Размерность представляет собой квадрат размерности случайной функции: 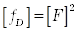 .
.
 Distribution = rootMeanSquare:
Distribution = rootMeanSquare:Функция распределения среднего квадратического значения по полосам шкалы спектра 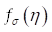 . Размерность совпадает с размерностью случайной функции:
. Размерность совпадает с размерностью случайной функции: 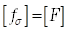 .
.
function DistributionFunction
Функция распределения.
scalar x0
Начальное значение аргумента случайной функции.
scalar deltax
Интервал, на котором генерируется случайная функция.
Необязательные именованные параметры метода
 randomDetail = scalar [-]
randomDetail = scalar [-]Количество точек на волне для максимальной частоты. По умолчанию randomDetail=8.
 randomType = scalar [-]
randomType = scalar [-]Тип распределения. 0 – случайное распределение, 1, …, 4 – псевдослучайное распределение. По умолчанию randomType = 0.
Описание
Заданная пользователем шкала спектра SpectralScale определяет полосы спектра, используемого для представления функции в виде ряда Фурье. Далее будем считать, что полосы заданы границами по частоте 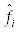 или угловой частоте
или угловой частоте  (
(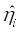 – общее обозначение) в зависимости от флага Frequency. При этом стоит отметить, что единицы измерения
– общее обозначение) в зависимости от флага Frequency. При этом стоит отметить, что единицы измерения 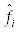 и
и  могут отличаться от общепринятых (
могут отличаться от общепринятых (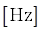 и
и 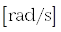 , соответственно). Размерность аргумента функции зависит от того, как интерпретируются значения шкалы спектра:
, соответственно). Размерность аргумента функции зависит от того, как интерпретируются значения шкалы спектра: 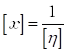 , если
, если  , и
, и 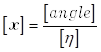 , если
, если 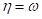 .
.
Метод создает случайную функцию 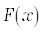 на интервале
на интервале 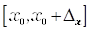 , где параметры
, где параметры 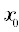 и
и 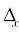 задаются пользователем. Функция представляется в виде ряда Фурье по заданному пользователем спектру:
задаются пользователем. Функция представляется в виде ряда Фурье по заданному пользователем спектру:
где 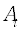 – амплитуда, соответствующая
– амплитуда, соответствующая  -ой полосе спектра,
-ой полосе спектра, 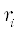 – случайная величина со значениями от 0 до 1,
– случайная величина со значениями от 0 до 1, 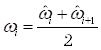 – угловая частота, соответсвующая центру
– угловая частота, соответсвующая центру  -ой полосы спектра. Суммирование осуществляется по всем полосам спектра.
-ой полосы спектра. Суммирование осуществляется по всем полосам спектра.
Отметим, что функции распределения для амплитуды 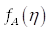 , дисперсии
, дисперсии 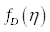 и среднего квадратического значения
и среднего квадратического значения 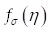 задаются по полосам шкалы спектра. Соответствующие параметры для каждой полосы вычисляются в её центре и используются как дискретные значения.
задаются по полосам шкалы спектра. Соответствующие параметры для каждой полосы вычисляются в её центре и используются как дискретные значения.
Если задается функция распределения амплитуды по полосам шкалы спектра 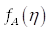 (позиционный параметр Distribution = amplitude:), то амплитуда
(позиционный параметр Distribution = amplitude:), то амплитуда  -ой полосы спектра вычисляется по формуле (см. Рис. 13):
-ой полосы спектра вычисляется по формуле (см. Рис. 13):
где 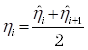 – центр
– центр  -ой полосы спектра.
-ой полосы спектра.
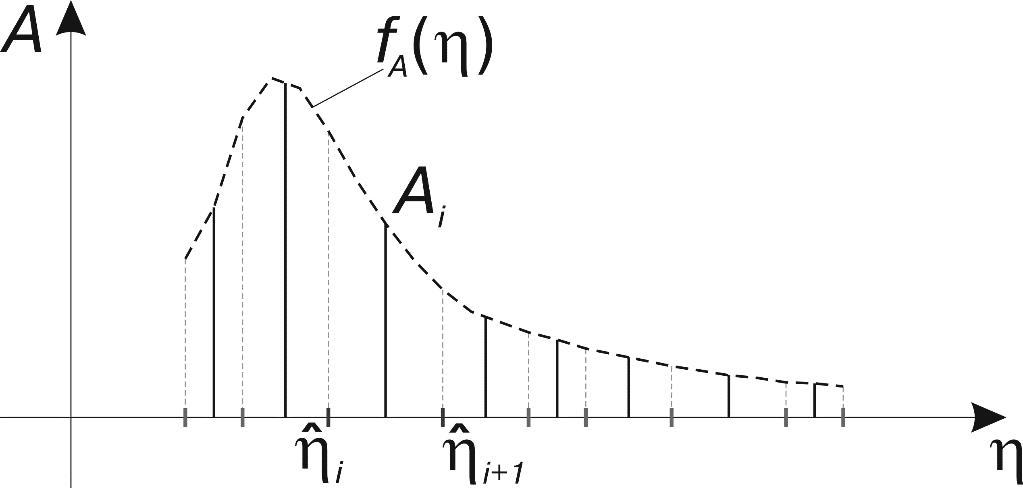
Рис. 13. Функция распределения амплитуды по полосам шкалы спектра
Если задается функция распределения дисперсии по полосам шкалы спектра 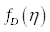 (позиционный параметр Distribution = dispersion:), то амплитуда
(позиционный параметр Distribution = dispersion:), то амплитуда  -ой полосы спектра вычисляется по формуле:
-ой полосы спектра вычисляется по формуле:
где 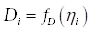 – дисперсия
– дисперсия  -ой полосы спектра.
-ой полосы спектра.
Если задается функция распределения среднего квадратического значения по полосам шкалы спектра 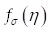 (позиционный параметр Distribution = rootMeanSquare:]), то амплитуда
(позиционный параметр Distribution = rootMeanSquare:]), то амплитуда  -ой полосы спектра вычисляется по формуле:
-ой полосы спектра вычисляется по формуле:
где 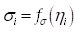 – среднее квадратическое значение
– среднее квадратическое значение  -ой полосы спектра.
-ой полосы спектра.
Плотность распределения в отличие от других типов функций распределения представляется в виде непрерывной функции по частоте 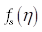 (позиционный параметр Distribution = density:). Амплитуда
(позиционный параметр Distribution = density:). Амплитуда  -ой полосы спектра вычисляется по формуле:
-ой полосы спектра вычисляется по формуле:
где 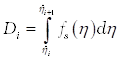 – дисперсия
– дисперсия  -ой полосы спектра.
-ой полосы спектра.
Для ускорения расчета значения функции 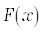 насчитываются только на интервале
насчитываются только на интервале 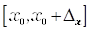 , заданном пользователем, и на сетке по аргументу
, заданном пользователем, и на сетке по аргументу 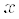 с шагом
с шагом 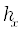 , определяемым количеством точек на волне для максимальной частоты
, определяемым количеством точек на волне для максимальной частоты  (параметр randomDetail):
(параметр randomDetail): 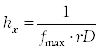 , где
, где 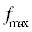 – правая граница диапазона частот. За пределами диапазона
– правая граница диапазона частот. За пределами диапазона 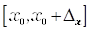 функция полагается равной нулю.
функция полагается равной нулю.
Пример
// случайная функция whiteNoiseLin определяется на интервале от 0 до 10 [s]
// на линейной шкале спектра (центры полос от 1 до 500 [Hz] с шагом 1[Hz])
// с постоянной плотностью распределения
spectralScale spScaleLin=linear( simpleMean:, 1, upperBound = 500, bandsN = 500, frequencyUnit = "[Hz]" );
function Dens=1[s];
function whiteNoiseLin=random1( frequency:, spScaleLin, density:, Dens, 0 [s], 10 [s] );