2.2.20 Белый шум
Данный метод создает белый шум – случайную функцию на заданном интервале, характеризующуюся постоянной функцией плотности во всем диапазоне заданных частот. Для задания пользователем используется среднее квадратическое значение функции, которое в дальнейшем пересчитывается в плотность. Функция имеет один аргумент.Функция определяется только на заданном интервале по аргументу; это используется для ускорения расчета. За пределами этого интервала функция полагается равной нулю. Математическое ожидание случайной функции равно нулю.
Под частотой понимается величина, обобщенная на случай произвольной размерности аргумента функции (см. раздел «Шкала спектра (spectralScale)» главы «Служебные объекты»).
Синтаксис метода создания
whiteNoise(sigma, x1, x2, fmin, fmax, spectrType = …, bandsN = …, randomDetail = …, randomType = …)
Обязательные позиционные параметры метода
scalar sigma
Среднее квадратическое значение случайной функции. Размерность совпадает с итоговой размерностью случайной функции.
scalar x1
Начальное значение аргумента случайной функции.
scalar x2
Конечное значение аргумента случайной функции.
scalar fmin
Значение частоты, соответствующее нижней границе спектра. Размерность – обратная размерности аргумента.
scalar fmax
Значение частоты, соответствующее верхней границе спектра частот.
Необязательные именованные параметры метода
spectrType = [linear:/logarithmic:]
Параметр тип шкалы спектра: линейная или логарифмическая. По умолчанию используется логарифмическая шкала spectrType = logarithmic:.
spectrType = linear:Линейная шкала спектра.
spectrType = logarithmic:Логарифмическая шкала спектра.
bandsN = scalar [-]Число полос спектра. По умолчанию bandsN = 100.
randomDetail = scalar [-]Количество точек на волне для максимальной частоты. По умолчанию randomDetail=8.
randomType = scalar [-]Тип распределения. 0 – случайное распределение, 1, …, 4 – псевдослучайное распределение. По умолчанию randomType = 0.
Описание
Заданный интервал частот [fmin, fmax] разбивается на полосы спектра, используемого для представления функции в виде ряда Фурье. Спектр используется линейный или логарифмический в зависимости от флага spectrType; величины fmin и fmax трактуются как центры крайних полос. Центры полос спектра обозначим как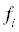 
, а границы – 
.
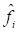, а границы – .Плотность распределения по частоте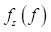 
вычисляется по среднему квадратическому значению 
и является постоянной для всех частот:
вычисляется по среднему квадратическому значению 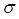и является постоянной для всех частот:
.Метод создает случайную функцию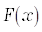 
на интервале 
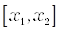, где параметры 
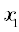и 
задаются пользователем. Функция представляется в виде ряда Фурье по спектру:
на интервале , где параметры и 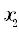задаются пользователем. Функция представляется в виде ряда Фурье по спектру:
, 
,где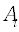 
– амплитуда, соответствующая 
-ой полосе спектра, 
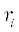– случайная величина со значениями от 0 до 1, 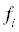– центр -ой полосы спектра. Суммирование осуществляется по всем полосам спектра.
– амплитуда, соответствующая -ой полосе спектра, – случайная величина со значениями от 0 до 1, – центр -ой полосы спектра. Суммирование осуществляется по всем полосам спектра.Амплитуда -ой полосы спектра вычисляется по формуле:
-ой полосы спектра вычисляется по формуле:
.Для ускорения расчета значения функции 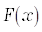насчитываются только на интервале 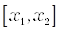, заданном пользователем, и на сетке по аргументу 
с шагом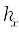 
, определяемым количеством точек на волне для максимальной частоты 
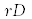(параметр randomDetail): 
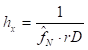, где 
– правая граница спектра частот. За пределами диапазона функция равна нулю.
насчитываются только на интервале , заданном пользователем, и на сетке по аргументу с шагом , определяемым количеством точек на волне для максимальной частоты (параметр randomDetail): , где 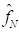– правая граница спектра частот. За пределами диапазона 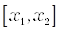функция равна нулю.