7.3 Характеристики жесткости элементов модели колеса

В моделях колеса «шина-EULER-M1» и «шина-EULER-M2» предполагается, что центр кольца брекера не смещается относительно центра обода в радиальном направлении. поэтому в данном случае считается, что нормальная деформация шины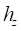

является деформацией кольца относительно опорной поверхности

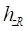, то есть

.

В модели колеса «шина-EULER-M3»

, (2)

где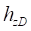

– радиальное смещение центра кольца относительно центра обода.

В модели колеса «шина-EULER-M3» принято

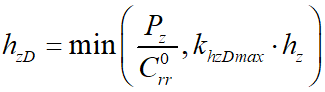(3)

где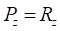

– радиальная сила, действующая на кольцо (обод) со стороны опорной поверхности;

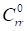– коэффициент жесткости радиального смещения кольца относительно обода при малых деформациях;

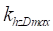– предельная доля смещения кольца относительно обода по отношению к нормальной деформации шины. В модели принято

.

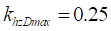Характеристики жесткости элементов модели колеса определяются в условиях действия на нее номинальной нагрузки, при малых деформациях и без проскальзывания элементов шины по опорной поверхности. На рис.11 приведена модель шины, используемая для расчета жесткостных характеристик, которая разбита на n дисков.

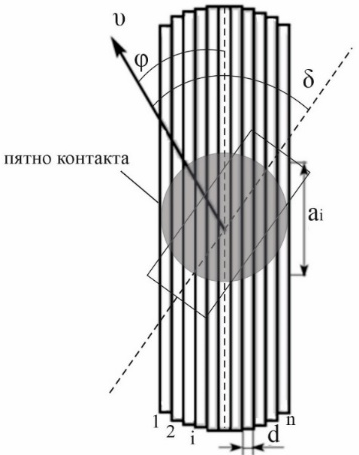
Рис. 11. Схема бокового увода дискретизованной шины

На рис.11 приведены:

−

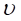– линейная скорость колеса;

−

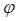– угловое смещение кольца колеса относительно линейной скорости колеса в опорной плоскости;

−

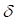– угол между проекцией линейной скорости колеса на опорную плоскость и его продольной осью.

Последовательность вычислений для получения жесткостных характеристик шины приведена ниже.

По определению коэффициент сопротивления увода шины

, (4)

где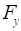

– боковая сила колеса, действующая в направлении оси Y.

Боковая сила, действующая в направлении оси Y, приложенная на каждый i-ый дискретный диск модели шины, вычисляется по формуле:

.

Таким образом суммарная боковая сила колеса равна

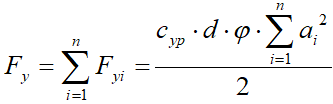. (5)

Подставляя (5) в (4) получаем

.

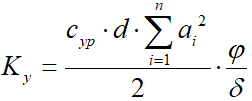Откуда

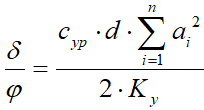. (6)

Согласно рис.11 жесткость углового смещения кольца относительно обода вычисляется по формуле:

, (7)

где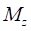

– стабилизирующий момент колеса, действующий вокруг оси Z.

Стабилизирующий момент, действующий вокруг оси Z, приложенный на каждый

i-ый дискретный диск модели шины, вычисляется по формуле

.

Откуда

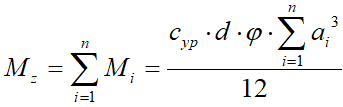. (8)

После подстановки (8) в (7) получим

.

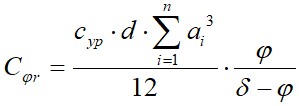Откуда

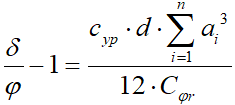. (9)

Подставляя (6) в (9) получаем

.

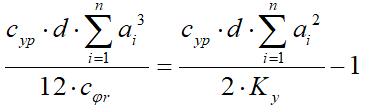Откуда боковая жесткость единицы площади протектора шины:

,

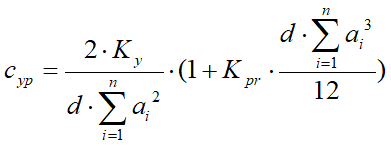где

.

Согласно распределению жесткостей колеса в поперечном направлении (рис.9)

, (10)

, (11)

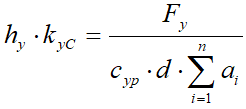. (12)

Разделив (11) на (12) получим

.

Откуда

,

.

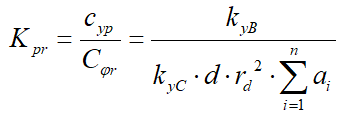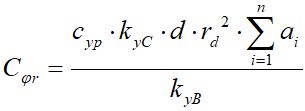Из (12) следует, что коэффициент суммарной боковой жесткости колеса

.

Разделив (12) на (10) получим

.

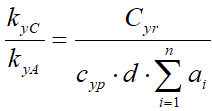Откуда

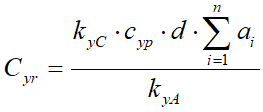или

.

Согласно распределению продольного смещения между элементами модели шины (рис.10)

, (13)

, (14)

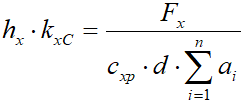, (15)

где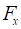

– продольная сила колеса, действующая в направлении оси X.

Из (13) следует, что

.

Также коэффициент суммарной продольной жесткости колеса

.

Из (14) следует, что

.

Из (15) следует, что коэффициент суммарной продольной жесткости колеса

.

Откуда продольная жесткость единицы площади протектора шины

.

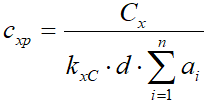При расчете модели колеса «шина-EULER-M2» используются жесткости сдвига протектора относительно обода колеса в боковом и продольном направлениях, приходящиеся на единицу площади контакта шины, которые могут быть рассчитаны по следующим формулам:

, (16)

. (17)