7.4 Предварительные вычисления вспомогательных зависимостей
Согласно схеме взаимодействия колеса с опорной поверхностью (рис.7) шина взаимодействует с ней с помощью упругих элементов, расположенных на кольце брекера, соответственно, при расчете и использовании предварительно рассчитанных таблиц характеристик шины должны использоваться параметры положения кольца. На стадии предварительных вычислениях при этом также необходимо учитывать, что в моделях колеса «шина-EULER-M1» и «шина-EULER-M2» звено кольца брекера жестко связывается со звеном обода.
Шина представляется как симметричное пространственное тело, полученное вращением линии профиля недеформированной шины вокруг оси вращения кольца. В расчетной модели шина разбивается на элементы, как это показано на рис.12. В направлении оси вращения шина равномерно разбивается на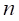 
цилиндрических секций толщины 
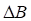, так, чтобы середины боковых поверхностей цилиндрических секций лежали на линии профиля шины. В радиальном направлении шина равномерно разбивается плоскостями перпендикулярными ее центральной плоскости вращения и проходящими через ось вращения кольца, на 
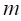секторов.
цилиндрических секций толщины , так, чтобы середины боковых поверхностей цилиндрических секций лежали на линии профиля шины. В радиальном направлении шина равномерно разбивается плоскостями перпендикулярными ее центральной плоскости вращения и проходящими через ось вращения кольца, на секторов.
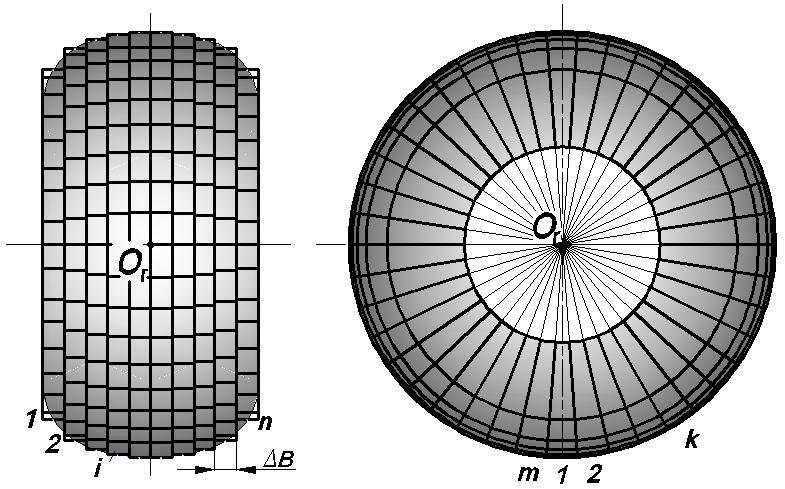
Рис. 12. Разбиение шины на элементы
Перед расчетом силового взаимодействия шины с опорной поверхностью производится вычисление следующих вспомогательных зависимостей:
; (18)
; (19)
; (20)
; (21)
; (22)
; (23)
; (24)
; (25)
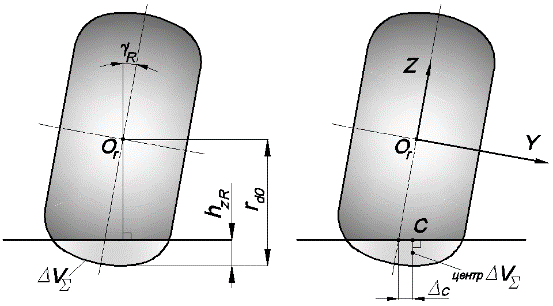
, (26)где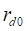 
– расстояние, замеренное по нормали к опорной плоскости от центра кольца до самой дальней точки профиля шины в центральной поперечной плоскости (рис.13а);
– расстояние, замеренное по нормали к опорной плоскости от центра кольца до самой дальней точки профиля шины в центральной поперечной плоскости (рис.13а);
– суммарный объем деформации шины, под которым понимается объем отсекаемый бесконечной плоскостью от геометрического тела, представляющего недеформированную шину;
– угол наклона кольца брекера;
– нормальная деформация кольца относительно опорной поверхности;
– нормальная нагрузка на колесо;
– объемная плотность статической реакции опорной поверхности;
– смещение центра 
пятна контакта вдоль поперечной оси пятна контакта относительно проекции центра кольца 
на опорную плоскость вдоль вертикальной оси кольца (рис.13б);
– радиус профиля шины в сечении плоскостью параллельной центральной плоскости вращения кольца и проходящей от нее на расстоянии 
(рис.13в);
– площадь деформации сектора в плоскости биссектрисы его центрального угла (рис.13г);
– смещение центра площади деформации сектора шины вдоль оси вращения кольца (рис.13г).
 |
 |
|
а) б)
|
в) г)
|
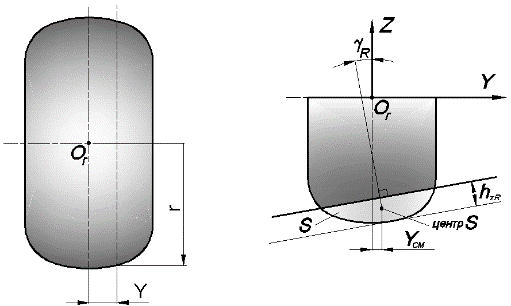
Рис. 13. Параметры вспомогательных зависимостей
Для задания характеристик (18)-(20), (23)-(26) используются геометрические размеры ненагруженной шины. Для задания характеристик (21), (22) помимо геометрических размеров используется упругая характеристика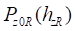 
, представляющая собой зависимость нормальной статической нагрузки 
на кольцо (
), установленное с нулевым углом наклона, от вертикального прогиба кольца, полученную при обжатии шины на плоскости.
, представляющая собой зависимость нормальной статической нагрузки 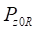на кольцо (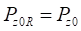), установленное с нулевым углом наклона, от вертикального прогиба кольца, полученную при обжатии шины на плоскости.При построении характеристики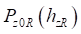 
для меняющегося с заданным шагом значения прогиба кольца 
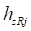определяется соответствующая ему величина прогиба обода 
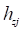и соответствующая сила 
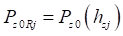, где 
– упругая характеристика шины.
для меняющегося с заданным шагом значения прогиба кольца определяется соответствующая ему величина прогиба обода и соответствующая сила , где 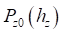– упругая характеристика шины.Для моделей «шина-EULER-M1» и «шина-EULER-M2»:
.Для модели «шина-EULER-M3» с учетом (2), (3) получаем уравнение, связывающее 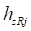с :
с :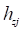
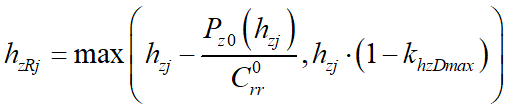,где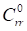 
– коэффициент жесткости радиального смещения кольца при малых деформациях.
– коэффициент жесткости радиального смещения кольца при малых деформациях.Зависимость 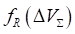получается из предположения радиального направления элементарных статических реакций 
в пределах пятна контакта 
-й цилиндрической секции шины (рис.14).
получается из предположения радиального направления элементарных статических реакций 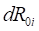в пределах пятна контакта 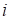-й цилиндрической секции шины (рис.14).
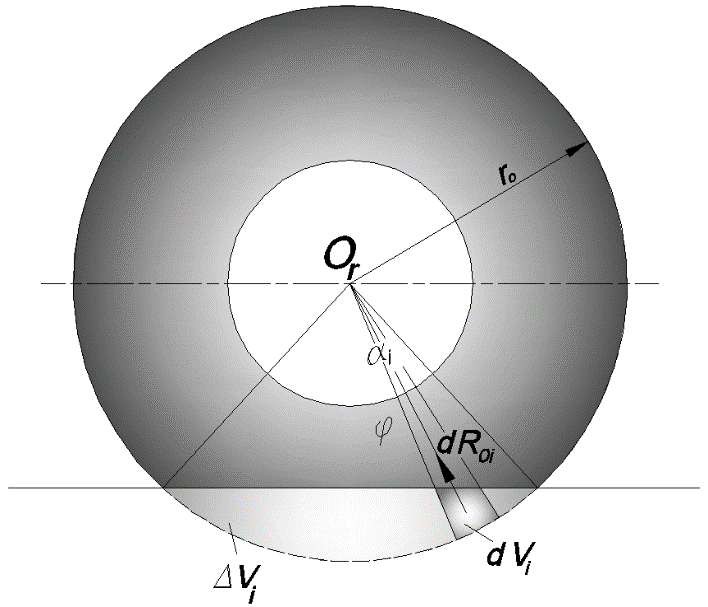
Рис. 14. К определению статических реакций в 
-й цилиндрической секции
-й цилиндрической секцииЭлементарная статическая реакция в -й цилиндрической секции шины вычисляется по формуле:
-й цилиндрической секции шины вычисляется по формуле:
,где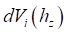 
– элементарный объем деформации шины в -й цилиндрической секции шины.
– элементарный объем деформации шины в 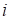-й цилиндрической секции шины.Нормальная статическая реакция в 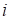-й цилиндрической секции:
-й цилиндрической секции:
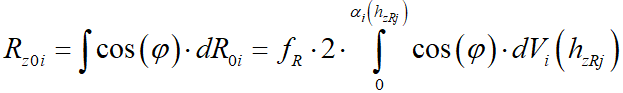,где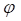 
– угол между биссектрисой центрального угла элементарного сектора шины в пределах пятна контакта и нормалью к опорной плоскости; 
– угол между радиусом, проведенным из крайней точки пятна контакта и нормалью к опорной поверхности в средней поперечной плоскости -й цилиндрической секции.
– угол между биссектрисой центрального угла элементарного сектора шины в пределах пятна контакта и нормалью к опорной плоскости; 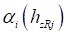– угол между радиусом, проведенным из крайней точки пятна контакта и нормалью к опорной поверхности в средней поперечной плоскости 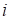-й цилиндрической секции.Сумма нормальных статических реакций по всем цилиндрическим секциям равна нормальной статической нагрузке на кольцо. Соответственно объемная плотность статической реакции опорной поверхности определяется следующим образом:
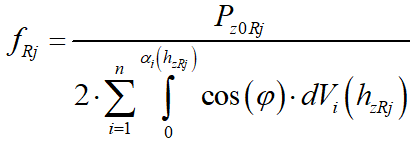,где 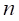– число цилиндрических секций шины.
– число цилиндрических секций шины.