3.1 Основные определения и механические свойства
Концепция представления элементарной площадки движителя
Под движителем транспортного средства понимается поверхность, контактирующая с деформируемым основанием. Для расчета взаимодействия движителя с грунтом контактирующая поверхность аппроксимируется набором элементарных площадок движителя (ЭПД), каждая из которых представляет собой плоскую ограниченную область. Данная площадка может быть частью поверхности шины, гусеницы, а также других подобных объектов. Один из простейших вариантов возможного разбиения поверхности шины представлен на рис. 1.
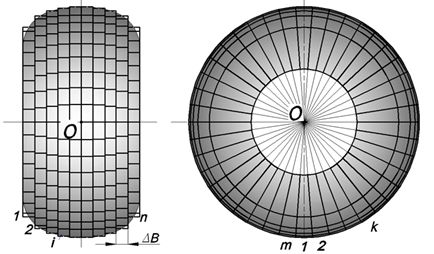

Рис. 1. Разбиение поверхности шины
на элементарные площадки движителя
Определение геометрии деформируемого основания
Принято, что поверхность грунта определяется суммой его макро- и микрогеометрии (рис. 2). Для задания основной (макро) геометрии деформируемого основания используется понятие базовой поверхности. Базовая поверхность определяет макропрофиль деформируемого основания, по ней вычисляется нормаль, необходимая для определения направления действующих на элементарную площадку движителя сил. В рамках данной модели будем полагать, что нормаль в процессе деформирования грунта не пересчитывается.
Для описания геометрии базовой поверхности вводится собственное параметрическое представление вида 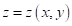 в системе координат узла, связанного с деформируемым основанием (узел дороги). По умолчанию данная функция равна нулю, что соответствует плоскому макропрофилю грунта. Система координат узла дороги представляет собой ортонормированный базис, переход от которого к системе координат проекта (СКП) осуществляется с помощью соответствующей матрицы поворота.
в системе координат узла, связанного с деформируемым основанием (узел дороги). По умолчанию данная функция равна нулю, что соответствует плоскому макропрофилю грунта. Система координат узла дороги представляет собой ортонормированный базис, переход от которого к системе координат проекта (СКП) осуществляется с помощью соответствующей матрицы поворота.
Помимо основной геометрии грунта с целью задания микропрофиля используется дополнительная функция, определяющая высоту поверхности деформируемого основания над базовой поверхностью в аналогичной форме 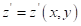 . По умолчанию данная функция также равна нулю, то есть микрорельеф отсутствует. Таким образом окончательный профиль поверхности определяется суперпозицией двух функций:
. По умолчанию данная функция также равна нулю, то есть микрорельеф отсутствует. Таким образом окончательный профиль поверхности определяется суперпозицией двух функций:
где 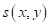 – функция, определяющая итоговую геометрию деформируемого основания.
– функция, определяющая итоговую геометрию деформируемого основания.
Данная функция должна иметь взаимно-однозначное соответствие между параметрами 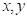 и ее значением. В результате заданной параметризации локальные векторы базиса поверхности принимают следующий вид:
и ее значением. В результате заданной параметризации локальные векторы базиса поверхности принимают следующий вид:
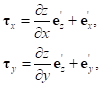 (2)
(2)где 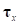 ,
, 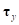 – локальные векторы базиса поверхности;
– локальные векторы базиса поверхности; 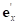 ,
, 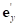 ,
, 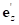 – ортонормированный базис, соответствующий локальной системе координат дороги. Тогда вектор нормали к поверхности имеет следующее выражение:
– ортонормированный базис, соответствующий локальной системе координат дороги. Тогда вектор нормали к поверхности имеет следующее выражение:
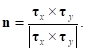 (3)
(3)Плоскость, образованную координатными линиями x и y (рис. 2), будем называть плоскостью параметризации деформируемого основания. В дальнейшем вместо аналитического применяется дискретное представление геометрии поверхности грунта. В частности, поверхность грунта разбивается на элементарные площадки (ЭПГ), которые имеют одинаковые размеры в проекции на плоскость параметризации.
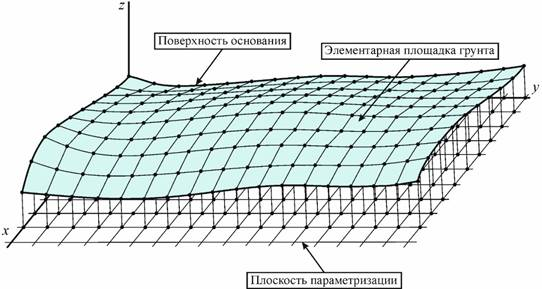
Рис. 2. Геометрия деформируемого основания
Механические свойства деформируемого основания
Механические свойства деформируемого основания необходимые для расчета определяются в рамках следующих характеристик:
− характеристика сопротивления грунта вдавливанию;
− характеристика сопротивления грунта сдвигу;
− критерий предельного состояния грунта;
− жесткость упругого сжатия грунта, отнесенная к единице площади;
− жесткость упругого сдвига грунта, отнесенная к единице площади;
− зависимость дополнительного погружения от деформации сдвига при буксовании.
На основании введенной ранее геометрии производится дискретизация поверхности грунта. Суммарное погружение колеса относительно уровня базовой поверхности можно представить в виде аддитивного разложения:
где 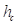 – деформация грунта вызванная только сжатием;
– деформация грунта вызванная только сжатием;
Аналогичный вид декомпозиции принимается и для сдвиговой деформации:
где 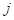 – суммарная деформация сдвига грунта;
– суммарная деформация сдвига грунта;
В процессе расчета взаимодействия движителя с деформируемым основанием для каждой точки базовой поверхности деформируемого основания данные параметры деформации вычисляются по завершению шага интегрирования и сохраняются, позволяя таким образом учитывать историю нагружения грунта.
Характеристика сопротивления грунта вдавливанию
Существует множество аналитических зависимостей, описывающих поведение грунта при сжатии, в частности, зависимости М.Н. Летошнева, М.Г. Беккера, А. Рииса, а также их модификации и обобщения. В программном комплексе EULER при расчете взаимодействия площадки движителя транспортного средства с грунтом деформируемого основания в качестве базовой характеристики изменения давления грунта при сжатии 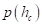 используется формула Беккера (рис. 3):
используется формула Беккера (рис. 3):
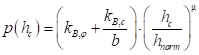 (6)
(6)где 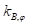 и
и 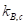 – модули внутреннего трения и сцепления;
– модули внутреннего трения и сцепления;
Повторное нагружение при вдавливании
Для расчета коэффициента нормальной жесткости деформированного уплотненного грунта 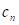 используется модель Вонга Дж.:
используется модель Вонга Дж.:
где 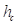 – глубина проникновения, при которой завершилось предыдущее погружение;
– глубина проникновения, при которой завершилось предыдущее погружение;
Обратите внимание – для большинства грунтов предлагается использовать 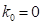 , что приводит к тому, что при малых погружениях
, что приводит к тому, что при малых погружениях 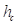 формула дает малые значения
формула дает малые значения 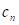 . В этом случае минимальное значение
. В этом случае минимальное значение 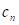 ограничено следующим соотношением
ограничено следующим соотношением 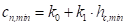 на интервале значений
на интервале значений 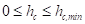 .
.
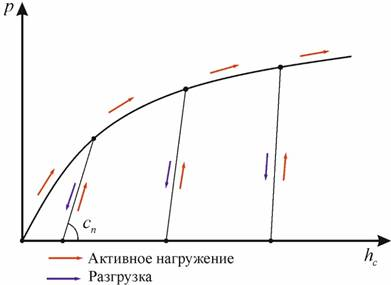
Рис. 3. Диаграмма вдавливания для грунта
Характеристика сопротивления грунта сдвигу
Другой важнейшей характеристикой сопротивления помимо сопротивления вдавливанию необходимой для расчетов является характеристика сопротивления сдвигу. В настоящее время разработано существенное количество моделей, описывающих поведение грунта при сдвиге, в частности, активно используются модели Z. Janosi, B. Hanamoto, Дж. Вонга, В.А. Комарова, а также их различные варианты. В программном комплексе EULER при расчете взаимодействия площадки движителя транспортного средства с грунтом деформируемого основания реализовано два варианта зависимостей. Первая из них – формула Вонга удобна для использования применительно к связным грунтам (рис. 4):
где 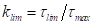 – отношение остаточного сопротивления сдвигу
– отношение остаточного сопротивления сдвигу 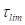 к максимальному;
к максимальному;
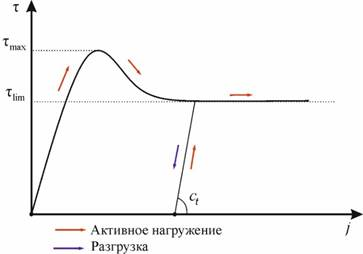
Рис. 4. Диаграмма сопротивления сдвигу по Вонгу
Второй вариант – зависимость Janosi, Hanamoto используется для описания сопротивления сдвигу сыпучих грунтов (рис. 5):
где 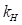 – эмпирический коэффициент.
– эмпирический коэффициент.
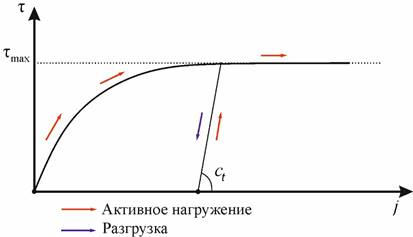
Рис. 5. Диаграмма сопротивления сдвигу Janosi, Hanamoto
Линия разгрузки при сдвиге для всех зависимостей соответствует коэффициенту удельной касательной жесткости деформированного грунта 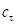 . Необходимые при расчете значения постоянных для типовых грунтов приведены в разделе Приложение.
. Необходимые при расчете значения постоянных для типовых грунтов приведены в разделе Приложение.
Критерий предельного состояния
Предполагается, что сопротивление грунта сдвигу (касательные напряжения сдвига в грунте) помимо накопленной деформации сдвига 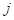 зависит также от давления
зависит также от давления  . В качестве критерия согласно которому определяется эта зависимость примем закон Кулона-Мора (рис. 6):
. В качестве критерия согласно которому определяется эта зависимость примем закон Кулона-Мора (рис. 6):
где 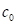 - внутреннее сцепление грунта;
- внутреннее сцепление грунта;
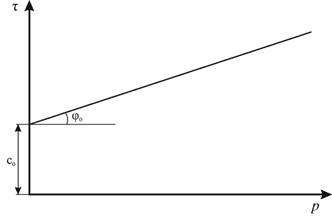
Рис. 6. Критерий Мора – Кулона
Внутреннее сцепление в грунтах определяется двумя факторами. С одной стороны, это структурное сцепление, обусловленное жесткими молекулярными связями между кристаллическими частями грунта. С другой стороны, внутреннее сцепление, зависящее от водно-коллоидных связей между частицами, что в наибольшей мере проявляется в связных грунтах типа глины. Коэффициент 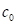 не зависит в явном виде от давления в грунте. Он характеризует свойство связности грунта. Для сыпучих грунтов он мал. Внутреннее трение в грунтах возникает в точках взаимного контакта твердых частиц и определяется угол внутреннего трения грунта
не зависит в явном виде от давления в грунте. Он характеризует свойство связности грунта. Для сыпучих грунтов он мал. Внутреннее трение в грунтах возникает в точках взаимного контакта твердых частиц и определяется угол внутреннего трения грунта 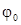 . Таким образом изменение предельного состояния в зависимости от давления (значение
. Таким образом изменение предельного состояния в зависимости от давления (значение 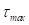 в формулах (8), (9)) определяется в расчете пропорционально текущему давлению согласно закону Мора-Кулона (10).
в формулах (8), (9)) определяется в расчете пропорционально текущему давлению согласно закону Мора-Кулона (10).
Зависимость дополнительного погружения от деформации сдвига при буксовании
При расчете взаимодействия площадки движителя транспортного средства с грунтом деформируемого основания в качестве зависимости дополнительного погружения от деформации сдвига при буксовании используется модифицированная зависимость М.Г. Беккера, в приращениях данная формула может быть представленная в следующем виде:
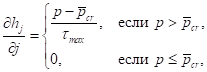 (11)
(11)где 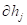 – элементарное приращение дополнительного погружения при буксовании;
– элементарное приращение дополнительного погружения при буксовании;
где 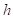 – текущее полное погружение в грунт;
– текущее полное погружение в грунт;
При этом, если 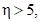 то
то 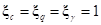 , а само
, а само 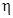 :
:
где 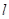 – длина штампа.
– длина штампа.
Коэффициенты несущей способности 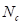 ,
, 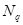 ,
, 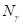 могут быть определены из таблиц или вычислены по следующим формулам [17, с.30-31]:
могут быть определены из таблиц или вычислены по следующим формулам [17, с.30-31]:
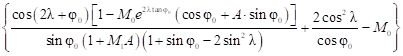 ,
,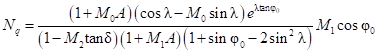 ,
,где 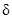 – угол наклона равнодействующей предельного давления к вертикали;
– угол наклона равнодействующей предельного давления к вертикали;
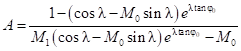 ;
;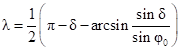 ;
;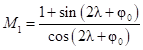 ;
;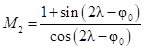 .
.