3.2 Расчет взаимодействия элементарной площадки движителя с деформируемым основанием
Расчет динамики контактного взаимодействия элементарной площадки можно разделить на несколько последовательных этапов (рис. 7).

Рис. 7. Схема расчета контактного взаимодействия ЭПД и ЭПГ
Проецирование поверхности ЭПД на поверхность грунта
На первом этапе осуществляется проецирование элементарной площадки движителя на поверхность грунта. Направление проецирование при этом перпендикулярно плоскости параметризации (рис. 8), что с учетом типа параметризации поверхности грунта принято называть z-проецированием. Проецирование необходимо для определения точек грунта, которые располагаются в проекции площадки движителя и потенциально могут вступить в контакт.
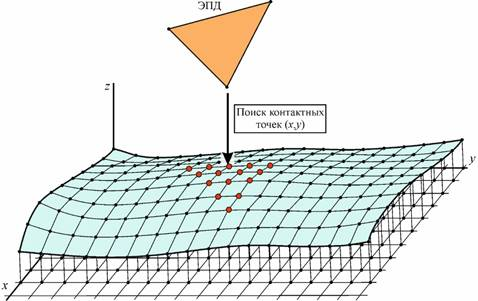
Рис. 8. Схема проецирования поверхности ЭПД на поверхность грунта
Математически данная процедура сводится к определению точек (узлов) регулярной сетки, попадающих в контур границы элементарной площадки. В ПК EULER принято использовать в качестве геометрии контактной площадки параметризованные простые поверхности конечных размеров: круг, треугольник и четырехугольник. В данном случае все дальнейшие выкладки подразумевают проекцию ЭПД на плоскость параметризации грунта, то есть поиск точек, принадлежащих контуру формулируется как задача двумерной геометрии.
Для треугольной площадки условие попадания точки внутрь области треугольника будем формировать на основе понятия барицентрических координат. Согласно свойству барицентрических координат известно, что если точка лежит внутри треугольника, то все координаты в барицентрической системе положительные. Барицентрические координаты геометрически представляют собой площади треугольников с вершиной в исследуемой точке (рис. 9), для которых выполняется следующие условия:
где 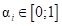 – барицентрические координаты;
– барицентрические координаты;
Из соотношений (13) получим следующее выражение для барицентрических координат:
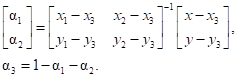 (14)
(14)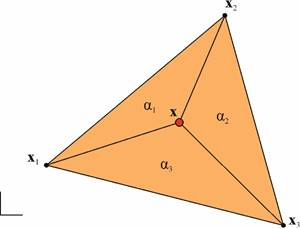
Рис. 9. Барицентрические координаты треугольника
Для четырехугольной площадки примем аналогичную параметризацию. В таком случае условие принадлежности точки четырехугольнику также означает, что все координаты принимают значения в диапазоне между 0 и 1. Связь между декартовыми и параметрическими координатами выглядит следующим образом:
где 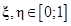 – параметрические координаты;
– параметрические координаты;
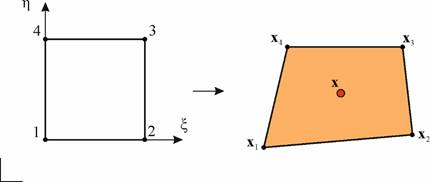
Рис. 10. Барицентрическая параметризация четырехугольника
Для получения барицентрических координат запишем выражение (15) в канонической форме:
где 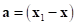 ,
,
Выражение (16) представляет собой нелинейное уравнение в векторной форме. Для нахождения неизвестных будем использовать метод Ньютона. В таком случае получим выражение для барицентрических координат в итерационном виде:
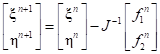 , (17)
, (17)где 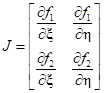 – якобиан, вычисляемый на каждой итерации.
– якобиан, вычисляемый на каждой итерации.
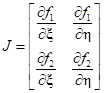 – якобиан, вычисляемый на каждой итерации.
– якобиан, вычисляемый на каждой итерации.Далее приведем соотношения для соответствующих производных:
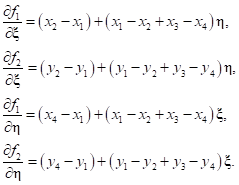 (18)
(18)Для простейших случаев контакта плоской поверхности, когда площадь опоры имеет небольшие размеры по сравнению с размерами механической системы, целесообразно также использовать круглую элементарную площадку (рис. 11). Данная площадка фактически задается точкой – центром координатами 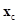 и радиусом Rmax.
и радиусом Rmax.
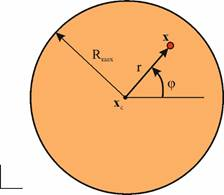
Рис. 11. Параметризация круглой площадки
Для круглой элементарной площадки при параметризации используется полярная система координат. Несмотря на то, что в этом случае форма и ориентация реальной контактной площадки не воспроизводится, в результате задача проецирования на поверхность грунта становится тривиальной.
Определение статуса контактного взаимодействия
После того как точки, потенциально находящиеся в контакте с элементарной площадкой определены, требуется определить статус контакта. Для этого необходимо осуществить обратное проецирование точек поверхности грунта на поверхность элементарной площадки (рис. 12).
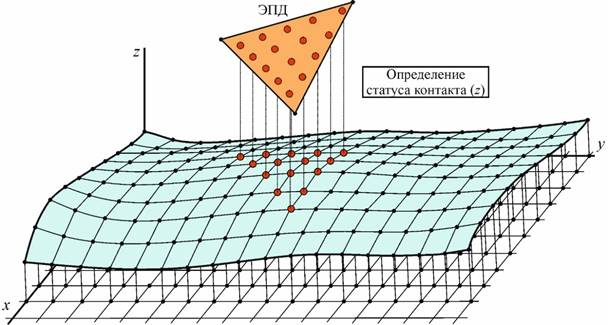
Рис. 12. Проецирование точек поверхности грунта
Так как локальные координаты точек грунта в системе ЭПД уже фактически были определены на предыдущем этапе, то для определения z-координаты необходимо воспользоваться следующим соотношениями (13) или (15) в зависимости от типа ЭПД. Для круглой площадки z-координата совпадает с координатой z ее центра. В результате для определения статуса контакта необходимо вычислить зазор между точками поверхности грунта и их проекция и на ЭПД:
где 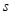 – координата z точки поверхности грунта,
– координата z точки поверхности грунта,
В случае если 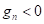 , то ЭПД находится в контакте с поверхностью грунта, в противном случае контакт отсутствует.
, то ЭПД находится в контакте с поверхностью грунта, в противном случае контакт отсутствует.
Расчет давления в узлах поверхности грунта
На следующем этапе с учетом найденного проникновения ЭПД в поверхность грунта, а также истории нагружения необходимо определить давление в точке грунта на текущем шаге интегрирования. Математически это означает, что необходимо найти 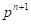 и
и 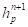 зная
зная 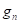 и
и 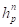 . Предлагаемая далее процедура аналогичная известной в теории пластичности процедуре проецирования напряжений на поверхность пластичности.
. Предлагаемая далее процедура аналогичная известной в теории пластичности процедуре проецирования напряжений на поверхность пластичности.
Для успешной ее адаптации применительно к подходу Беккера необходимо преобразовать экспериментальные зависимости 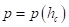 и
и 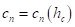 к виду
к виду 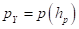 и
и 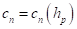 соответственно. То есть в исходных зависимостях необходимо выделить упругую и пластическую составляющие. Для этого удобно на первом этапе выделить начальный линейный упругий участок деформирования, который согласно выражениям (6), (7) фактически отсутствует. А также ограничить значение минимальной жесткости, которое согласно зависимости (7) теоретически может равняться нулю.
соответственно. То есть в исходных зависимостях необходимо выделить упругую и пластическую составляющие. Для этого удобно на первом этапе выделить начальный линейный упругий участок деформирования, который согласно выражениям (6), (7) фактически отсутствует. А также ограничить значение минимальной жесткости, которое согласно зависимости (7) теоретически может равняться нулю.
В случае если материал имеет нормальное упрочнение (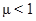 ), то упругий участок и минимальная жесткость будем ограничивать значением
), то упругий участок и минимальная жесткость будем ограничивать значением 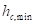 , которое является корнем уравнения:
, которое является корнем уравнения:
Данное уравнение нелинейное и решается методом Ньютона. Для грунта с аномальным упрочнением (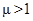 , такие значения обычно характерны для снега) упругий участок можно считать отсутствующим, а значение
, такие значения обычно характерны для снега) упругий участок можно считать отсутствующим, а значение 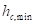 принять равным некоторому произвольному небольшому значению и воспринимать как величину ограничивающую только минимальную жесткость грунта в выражении (7).
принять равным некоторому произвольному небольшому значению и воспринимать как величину ограничивающую только минимальную жесткость грунта в выражении (7).
Перед расчетом контактного взаимодействия, необходимо осуществить упругую разгрузку грунта. На первом этапе, называемом «упругое приближение», приращение полной деформации численно равное зазору, определенному в результате проецирования на основе выражения (19), считается полностью упругим:
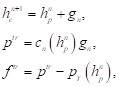 (21)
(21)где 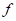 – функция текучести;
– функция текучести;
tr – индекс упругого приближения.
Если 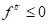 , значит активное нагружение отсутствует и первый шаг является окончательным:
, значит активное нагружение отсутствует и первый шаг является окончательным:
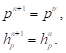 (22)
(22)В противном случае для 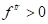 имеет место дополнительная пластическая деформация, следовательно необходима «коррекция»:
имеет место дополнительная пластическая деформация, следовательно необходима «коррекция»:
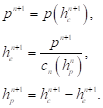 (23)
(23)По завершению шага интегрирования происходит сохранение значения пластической составляющей деформации вдавливания 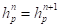 .
.
Расчет нормальных сил, определение эквивалентной плоскости контакта
После того как распределение давления в зоне контакта определено, необходимо его проинтегрировать по пятну контакта и рассчитать суммарные силы и моменты, действующие на движитель. Сила упругой нормальной реакции опорной поверхности определяется следующим образом:
где 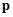 – вектор давления;
– вектор давления;
Коэффициент демпфирования определяется следующим образом:
где 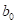 – коэффициент демпфирования при малых скоростях;
– коэффициент демпфирования при малых скоростях;
Интегрирование по пятну контакта будем осуществлять численно методом Гаусса по элементарным площадкам грунта, у которых хотя бы один из узлов имеет ненулевое значение давления (рис. 13).
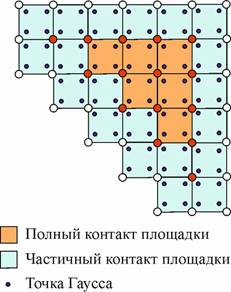
Рис. 13. Интегрирование по пятну контакта
Для удобства определим нормаль, а также введем параметрическое представление элементарной площадки грунта, выраженное линейными функциями формы (рис. 14):
где i – текущий номер узла в локальной нумерации;
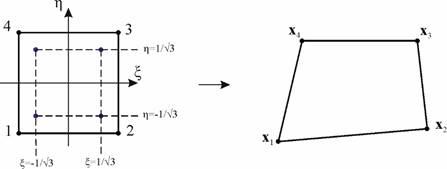
Рис. 14. Параметризация ЭПГ
Тогда абсолютную величину давления внутри элементарной площадки можно определить следующим образом:
Для выбранных функций формы достаточно второго порядка интегрирования, в результате получим квадратурные формулы для определения сил и моментов:
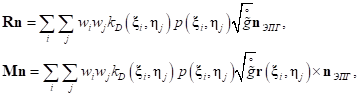 (28)
(28)где 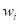 – весовые коэффициенты;
– весовые коэффициенты;
Далее приведем соотношения для соответствующих векторов касательного базиса:
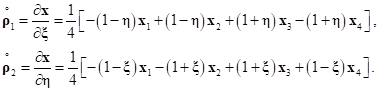 (29)
(29)После того как суммарное значение нормальных сил реакции опорной поверхности определены, введем понятие эквивалентной плоскости поверхности, которая задается интегральным значением нормали к поверхности грунта в пятне контакта 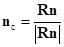 .
.
Расчет сопротивления сдвигу опорной поверхности и силы трения
На следующем этапе необходимо определить касательные усилия в контакте. Для этого сначала для точек грунта, находящихся в контакте с ЭПД, рассчитывается полная текущая деформация сдвига и ее приращение. Для определения новых значений деформации сдвига отслеживается перемещение проекции точки контакта на поверхности ЭПД на базовую поверхность (рис. 15). Под проекцией точек на базовую поверхность здесь и далее подразумевается проекция на эквивалентную плоскость, определяемую общей нормалью 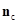 . Ниже рассмотрим особенности реализации данной процедуры.
. Ниже рассмотрим особенности реализации данной процедуры.
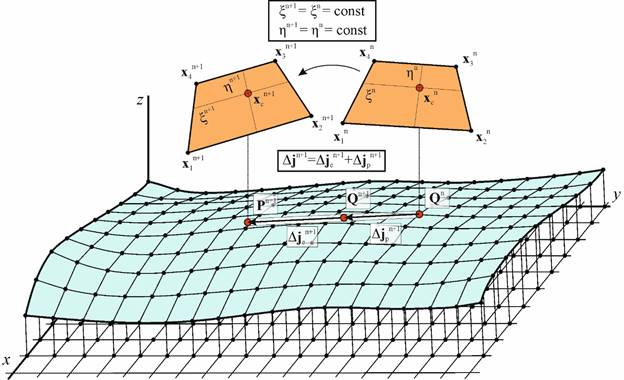
Рис. 15. Расчет деформации сдвига
На первом шаге, когда точка грунта впервые входит в контакт с ЭПД при расчете статуса контакта определяются локальные координаты (например, для четырехугольной площадки 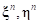 ) точки
) точки 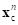 , соответствующей проекции точки грунта на ЭПД. Кроме того, запоминаем проекцию этой точки на поверхность грунта
, соответствующей проекции точки грунта на ЭПД. Кроме того, запоминаем проекцию этой точки на поверхность грунта 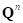 , координаты которой в момент первого контакта равны координатам одной из точек грунта. Далее будем отслеживать как движение точки контакта на ЭПД
, координаты которой в момент первого контакта равны координатам одной из точек грунта. Далее будем отслеживать как движение точки контакта на ЭПД 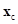 , так и ее первой проекции
, так и ее первой проекции 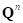 .
.
Далее в процессе интегрирования положение ЭПД меняется, в тоже время локальные координаты точки 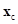 остаются постоянными во времени
остаются постоянными во времени 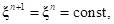
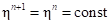 . Следовательно, воспользовавшись в данном случае соотношением (15), можно определить ее положение на текущем шаге интегрирования
. Следовательно, воспользовавшись в данном случае соотношением (15), можно определить ее положение на текущем шаге интегрирования 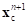 , а также ее проекцию на поверхность грунта
, а также ее проекцию на поверхность грунта 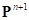 . Таким образом получим приращение деформации сдвига на текущем шаге интегрирования:
. Таким образом получим приращение деформации сдвига на текущем шаге интегрирования:
Отметим, что вектор полной деформации сдвига 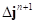 включает в себя как упругую так и пластическую составляющие, которые определяются согласно алгоритму проецирования изложенному далее. Кроме того, так сама процедура происходит вдоль единственного направления, соединяющего точки
включает в себя как упругую так и пластическую составляющие, которые определяются согласно алгоритму проецирования изложенному далее. Кроме того, так сама процедура происходит вдоль единственного направления, соединяющего точки 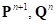 , то можно перейти от векторных параметров сдвига и напряжения в процедуре проецирования к скалярным.
, то можно перейти от векторных параметров сдвига и напряжения в процедуре проецирования к скалярным.
На следующем этапе с учетом найденного полного сдвига и его приращения в точке поверхности грунта, а также истории нагружения необходимо определить касательное напряжение в точке грунта на текущем шаге интегрирования, то есть требуется найти 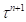 и
и 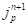 зная
зная 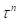 и
и 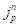 Данная процедура схожа с аналогичной реализованной ранее для определения давления. Так же как и в предыдущем случае для начала преобразуем экспериментальную зависимость
Данная процедура схожа с аналогичной реализованной ранее для определения давления. Так же как и в предыдущем случае для начала преобразуем экспериментальную зависимость 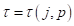 и к виду
и к виду 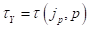 . Будем также предполагать, что силы трения удерживают контактную поверхность ЭПД и поверхность грунта от взаимных смещений.
. Будем также предполагать, что силы трения удерживают контактную поверхность ЭПД и поверхность грунта от взаимных смещений.
На первом этапе алгоритма будем считать найденное на основе (30) приращение деформации сдвига 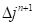 на текущем шаге полностью упругим:
на текущем шаге полностью упругим:
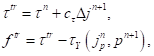 (31)
(31)где 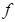 – функция текучести;
– функция текучести;
tr – индекс упругого приближения.
Если 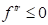 , значит активное нагружение отсутствует и первый шаг является окончательным:
, значит активное нагружение отсутствует и первый шаг является окончательным:
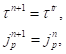 (32)
(32)В противном случае для 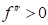 имеет место дополнительная пластическая деформация сдвига, следовательно необходима «коррекция»:
имеет место дополнительная пластическая деформация сдвига, следовательно необходима «коррекция»:
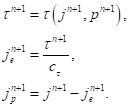 (33)
(33)После расчета необходимо проверить не превышает ли найденное напряжение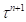 предельно возможное по сдвигу
предельно возможное по сдвигу
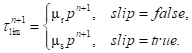 ,
,где 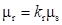 – коэффициент трения покоя;
– коэффициент трения покоя;
Таким образом, в случае превышения необходимо осуществить дополнительную коррекцию:
Отметим, что изменение значения логической переменной, равно как и значений внутренних переменных, характеризующих историю нагружения грунта при сдвиге, происходит по завершению шага интегрирования:
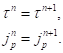 (35)
(35)Также при наличии пластической деформации осуществляется коррекция положения точки 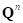 , на величину
, на величину 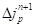 и в направлении сдвига определяемых вектором (30).
и в направлении сдвига определяемых вектором (30).
Другим важным моментом является сама процедура отслеживания деформации сдвига, корректная реализация которой предполагает процедуру перехода точки контакта от одной площадки движителя к другой (рис. 16), далее опишем суть данной процедуры.
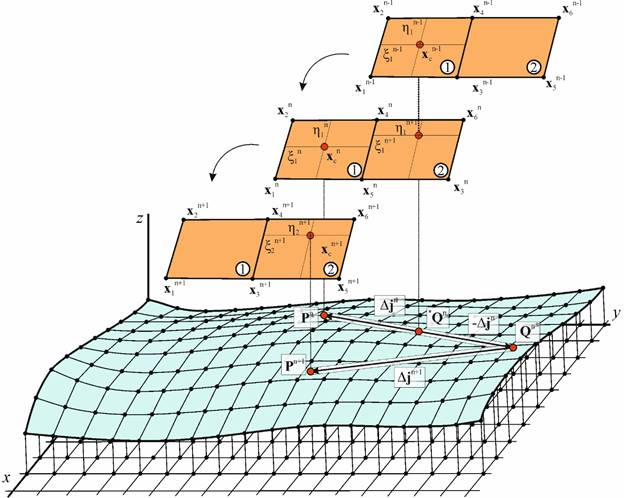
Рис. 16. Смещение проекции точки контакта
Предположим, что в момент времени 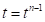 элементарная площадка движителя 1 входит в контакт в поверхностью грунта в точке
элементарная площадка движителя 1 входит в контакт в поверхностью грунта в точке 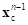 с локальными координатами
с локальными координатами 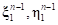 в результате определяется проекция
в результате определяется проекция 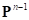 текущей точки контакта
текущей точки контакта 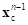 на эквивалентную плоскость. Так как точка грунта только вошла в контакт, то
на эквивалентную плоскость. Так как точка грунта только вошла в контакт, то 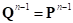 , следовательно, приращение деформации сдвига
, следовательно, приращение деформации сдвига 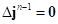 . На следующем шаге интегрирования в момент времени
. На следующем шаге интегрирования в момент времени 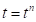 точка контакта на поверхности движителя продолжила движение и переместилась в положение
точка контакта на поверхности движителя продолжила движение и переместилась в положение 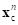 с проекцией
с проекцией 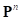 . С учетом положения точки контакта
. С учетом положения точки контакта 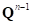 на прошлом шаге можно определить приращение деформации в момент времени
на прошлом шаге можно определить приращение деформации в момент времени 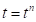 как
как 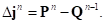 В то же время текущая проекция точки поверхности грунта находится на элементарной площадке 2 с локальными координатами
В то же время текущая проекция точки поверхности грунта находится на элементарной площадке 2 с локальными координатами 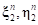 , следовательно на следующем шаге интегрирования будем отслеживать приращение деформации сдвига по движению проекции положения. Данная проекция в момент времени
, следовательно на следующем шаге интегрирования будем отслеживать приращение деформации сдвига по движению проекции положения. Данная проекция в момент времени 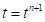 займет положение
займет положение 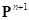 , однако в таком случае для корректного определения приращения необходимо при расчете деформации сдвига по формуле (30) использовать не точку
, однако в таком случае для корректного определения приращения необходимо при расчете деформации сдвига по формуле (30) использовать не точку 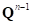 , а точку полученную смещением исходной на вектор противоположный приращению, полученному на шаге интегрирования:
, а точку полученную смещением исходной на вектор противоположный приращению, полученному на шаге интегрирования:
Данная процедура коррекции положения точки 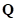 выполняется по завершению шага интегрирования и перед коррекцией на величину пластического сдвига (рис. 16).
выполняется по завершению шага интегрирования и перед коррекцией на величину пластического сдвига (рис. 16).
Расчет интегральных касательных сил, действующих на движитель
Интегральная сила касательной реакции опорной поверхности определяется следующим образом:
где 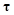 – вектор касательного напряжения;
– вектор касательного напряжения;
Процедура интегрирования аналогична приведенной выше для компоненты давления и приводит к следующим квадратурным соотношениям:
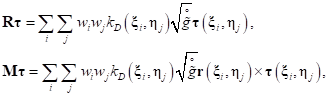 (38)
(38)Расчет дополнительного погружения при буксовании
Производная по времени дополнительного погружения за счет сдвига определяется следующим образом:
где 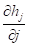 определяется формулой (11).
определяется формулой (11).
Угол 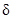 , от которого зависят коэффициенты несущей способности, определяем из соотношения:
, от которого зависят коэффициенты несущей способности, определяем из соотношения:
Коэффициенты несущей способности 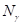 ,
, 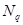 ,
,  при углах наклона к вертикали равнодействующей внешней нагрузки
при углах наклона к вертикали равнодействующей внешней нагрузки 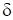 приведены в Таблице 1 (см. [16]).
приведены в Таблице 1 (см. [16]).
Расчет по формуле (12) допускается выполнять, если соблюдается условие:
Примечания:
1. При промежуточных значениях
2. В фигурных скобках приведены значения коэффициентов несущей способности, соответствующие предельному значению угла наклона нагрузки, исходя из условия (35).
|
Учет податливости элементарной площадки движителя
Ранее изложенный алгоритм рассматривался исходя из предположения, что элементарная площадка движителя является абсолютно жесткой. Несмотря на то, что грунт является достаточно податливым материалом, широко распространены движители, жесткостью которых нельзя пренебречь. В контексте данной модели податливость ЭПД выражается через нормальную жесткость 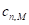 отнесенную к единице площади. Наличие нормальной жесткости ЭПД приводит к необходимости учета дополнительного упругого смещения при расчете нормальной реакции опорной поверхности, что в свою очередь означает введение итерационного процесса на шаге интегрирования.
отнесенную к единице площади. Наличие нормальной жесткости ЭПД приводит к необходимости учета дополнительного упругого смещения при расчете нормальной реакции опорной поверхности, что в свою очередь означает введение итерационного процесса на шаге интегрирования.