3.6 Особенности физических величин угла

Для удобства работы с угловыми величинами в EULER угол может измеряться (задаваться на входе и выводиться на пользователя) в радианах [rad] и градусах [deg].

В то же время в формулировках базовых физических законов угол принято выражать в радианах, но безразмерно. Физически это объяснимо, поскольку радианная мера угла представляет собой отношение длины дуги окружности к ее радиусу, то есть отношение длины к длине, что является безразмерной величиной.

Это можно проиллюстрировать на следующих примерах.

1. Уравнение динамики плоского вращательного движения твердого тела:

где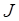

– момент инерции тела, размерность [mass length2];

– угловое ускорение тела, размерность [1/time2];

– момент сил, приложенных к телу, размерность [force length]=[mass length2/time2].

Размерности правой и левой части уравнения совпадают при безразмерном выражении угла. Если же размерность углового ускорения тела представить в виде [angle/time2], то согласованность правой и левой части уравнения нарушится.

2. Кинетическая энергия плоского вращательного движения твердого тела равна:

где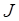

– момент инерции тела, размерность [mass length2];

– угловая скорость тела, размерность [1/time].

3. Угловая жесткость в теории упругости выражается следующей зависимостью:

где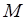

– момент действующих сил, размерность [force length];

– угловая деформация в радианах безразмерно.

Такие коэффициенты жесткости используются, например, в объекте EULER «матрица жесткости 6x6».



Отсюда необходимо сделать следующий вывод:

при записи в EULER формул, выражающих базовые физические законы, необходимо выражать угловые величины в радианах, но с приведением их к безразмерному виду. Например, при расчете кинетической энергии тела используется датчик угловой скорости с размерностью [angle/time]. Предварительно или непосредственно в выражении значение этого датчика необходимо разделить на один радиан.



В то же время следует отметить, что в целом ряде случаев в коэффициентах угловой жесткости и демпфирования могут использоваться размерные значения углов. Это более удобно для пользователя. Например, в силовом элементе «вращательный упругий элемент с коэффициентом жесткости» коэффициент угловой жесткости задается в размерности [force length/angle].