1.8.1 Параметры деформируемой втулки
 Шаблон используется при создании силового элемента деформируемая втулка и содержит ее упругие характеристики. Элемент является симметричным относительно продольной оси. Все силы и моменты, действующие на внутреннюю втулку, приложены в её геометрическом центре. Силы и моменты, действующие на внешнюю втулку, приложены, соответственно, в её геометрическом центре. К внутренней втулке привязана система координат
Шаблон используется при создании силового элемента деформируемая втулка и содержит ее упругие характеристики. Элемент является симметричным относительно продольной оси. Все силы и моменты, действующие на внутреннюю втулку, приложены в её геометрическом центре. Силы и моменты, действующие на внешнюю втулку, приложены, соответственно, в её геометрическом центре. К внутренней втулке привязана система координат 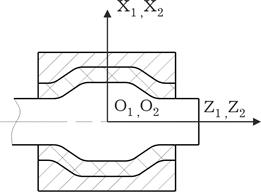
Рис. 1. Схема деформируемого шарнира
Синтаксис метода создания
silentblockParams(dFiZa, MZa, dAlfa, Malfa, dAlfamax, dZa, FZa, dZmax, dRa, FRa, dRmax, e)
Обязательные позиционные параметры метода
scalar dFiZa [angle]
Угол кручения, на котором начинается проскальзывание втулки вокруг продольной оси.
scalar MZa [force length]
Момент сопротивления кручению, соответствующий началу проскальзывания втулки вокруг продольной оси.
scalar dAlfa [angle]
Угол перекоса, на котором определен момент сопротивления перекосу.
scalar Malfa [force length]
Момент сопротивления перекосу, соответствующий углу перекоса dAlfa.
scalar dAlfamax [angle]
Предельный по обжатию материала угол перекоса (максимум 45°).
scalar dZa [length]
Осевое смещение, на котором определена продольная сила.
scalar FZa [force]
Продольная сила, определенная на смещении dZa.
scalar dZmax [length]
Предельное по обжатию материала осевое смещение.
scalar dRa [length]
Радиальное смещение, на котором определена поперечная сила.
scalar FRa [force]
Поперечная сила, определенная на смещении dRa.
scalar dRmax [length]
Предельное по обжатию материала радиальное смещение.
scalar e [-]
Эластичность связующего упругого материала по отскоку (коэффициент восстановления энергии).
Описание
Из данных проекта о взаимном положении и относительной скорости тел для элемента (с учетом начальных смещений и углов поворота) находятся:
Предполагается, что внутренняя втулка может прокручиваться относительно внешней вокруг продольной оси, если воздействие превышает заданное значение. При приложении сил или моментов по остальным направлениям существуют пределы смещений, поэтому для описания упругих характеристик используется асимптотическая функция, изображенная на рис. 2. Эта функция характеризуется пределом смещения 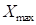 и жесткостью при нулевом смещении
и жесткостью при нулевом смещении 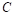 .
.
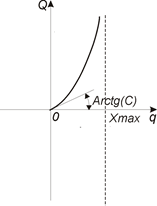
Рис. 2. Асимптотическая характеристика жесткости (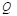 – усилие,
– усилие, 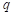 – смещение)
– смещение)
Усилия, действующие на внешнюю втулку, вычисляются следующим образом.
Продольная сила (действующая вдоль оси 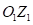 ):
):
Упругая 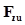 и демпфирующая
и демпфирующая 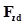 составляющие направлены вдоль оси
составляющие направлены вдоль оси 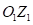 .
.
Их величины вычисляются следующим образом:
где 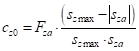 – осевая жесткость при нулевой деформации;
– осевая жесткость при нулевой деформации;
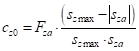 – осевая жесткость при нулевой деформации;
– осевая жесткость при нулевой деформации;Сила, действующая в плоскости 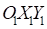 , вычисляется следующим образом:
, вычисляется следующим образом:
Упругая составляющая 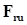 направлена вдоль вектора
направлена вдоль вектора 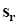 , который является проекцией радиус-вектора
, который является проекцией радиус-вектора 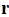 на плоскость
на плоскость 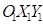 . Величина упругой составляющей вычисляется по формуле:
. Величина упругой составляющей вычисляется по формуле:
где 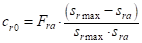 – радиальная жесткость при нулевой деформации;
– радиальная жесткость при нулевой деформации;
Демпфирующая составляющая 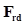 направлена вдоль вектора
направлена вдоль вектора 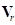 , который является проекцией на плоскость
, который является проекцией на плоскость 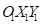 вектора скорости
вектора скорости 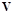 . Величина этой составляющей находится следующим образом:
. Величина этой составляющей находится следующим образом:
Момент сопротивления кручению 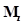 вычисляется по формуле:
вычисляется по формуле:
При кручении втулки вокруг оси 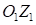 упругая составляющая
упругая составляющая 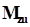 определяется аналогично элементу «Вращательное трение». До начала проскальзывания, определяемого достижением значения
определяется аналогично элементу «Вращательное трение». До начала проскальзывания, определяемого достижением значения 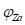 угловым смещением втулки, момент
угловым смещением втулки, момент 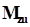 возрастает линейно. После достижения критического значения углового смещения начинается проскальзывание втулок друг относительно друга, и
возрастает линейно. После достижения критического значения углового смещения начинается проскальзывание втулок друг относительно друга, и 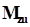 не увеличивается, оставаясь постоянным. Проскальзывание смещает характеристику упругой деформации. Таким образом, упругая
не увеличивается, оставаясь постоянным. Проскальзывание смещает характеристику упругой деформации. Таким образом, упругая 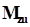 составляющая момента сопротивления кручению, вычисляется следующим образом:
составляющая момента сопротивления кручению, вычисляется следующим образом:
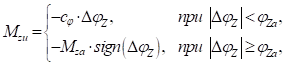
где 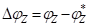 ;
;
Демпфирующая 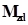 составляющая момента сопротивления кручению направлена вдоль оси
составляющая момента сопротивления кручению направлена вдоль оси 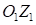 , и ее величина определяется выражением:
, и ее величина определяется выражением:
где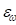 – малое пороговое значение угловой скорости.
– малое пороговое значение угловой скорости.
Момент сопротивления перекосу (лежащий в плоскости 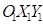 ):
):
Упругая составляющая 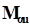 направлена вдоль вектора
направлена вдоль вектора 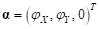 , и её величина вычисляется по формуле:
, и её величина вычисляется по формуле:
где 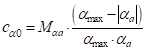 – жесткость на перекос при нулевой деформации;
– жесткость на перекос при нулевой деформации;
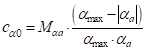 – жесткость на перекос при нулевой деформации;
– жесткость на перекос при нулевой деформации;Демпфирующая составляющая 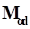 направлена вдоль вектора
направлена вдоль вектора 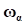 , который равен проекции угловой скорости
, который равен проекции угловой скорости 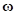 на плоскость
на плоскость 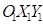 . Величина этой составляющей вычисляется по формуле:
. Величина этой составляющей вычисляется по формуле:
Силы, действующие на внутреннюю втулку, подчиняются третьему закону Ньютона