7.10.2 Расчет сил, действующих на обод со стороны кольца
Суммарный вектор сил, действующих на обод со стороны кольца, определяется следующим образом:
где 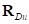 и
и 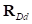 – упругая и демпфирующая составляющие суммарного вектора сил, действующих на обод со стороны кольца.
– упругая и демпфирующая составляющие суммарного вектора сил, действующих на обод со стороны кольца.
Жесткость радиального смещения кольца 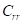 является нелинейной функцией радиальной деформации кольца относительно центра колеса
является нелинейной функцией радиальной деформации кольца относительно центра колеса 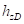 . В общем случае используя соотношения (16), (17) можно получить следующие формулы:
. В общем случае используя соотношения (16), (17) можно получить следующие формулы:
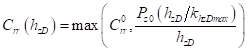 .
.В частном случае, когда имеет место (1), получим:
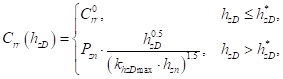 ,
, 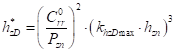 .
.Введем обозначения: 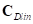 – вектор линейных жесткостей,
– вектор линейных жесткостей, 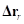 – линейное смещение кольца относительно обода,
– линейное смещение кольца относительно обода, 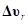 – линейная скорость смещения кольца относительно обода.
– линейная скорость смещения кольца относительно обода.
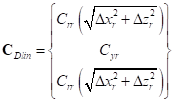 ,
, 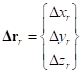 ,
, 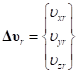 ,
,где 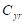 – коэффициент жесткости бокового смещения кольца;
– коэффициент жесткости бокового смещения кольца;
Тогда упругая составляющая суммарного вектора сил определяется по формуле: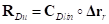 , где под операцией «
, где под операцией «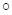 » понимается почленное перемножение векторов.
» понимается почленное перемножение векторов.
Демпфирующая составляющая суммарного вектора сил определяется следующим образом:
где 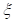 – коэффициент затухания колебаний кольца шины относительно обода (параметр может переопределяться пользователем; по умолчанию
– коэффициент затухания колебаний кольца шины относительно обода (параметр может переопределяться пользователем; по умолчанию 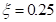 );
);
Суммарный вектор моментов сил, действующих на обод со стороны кольца, относительно центра колеса определяется по формуле: 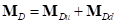 , где
, где 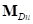 ,
, 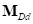 – упругая и демпфирующая составляющие суммарного вектора моментов сил, действующих на обод со стороны кольца.
– упругая и демпфирующая составляющие суммарного вектора моментов сил, действующих на обод со стороны кольца.
Введем обозначения: 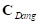 – вектор угловых жесткостей,
– вектор угловых жесткостей, 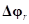 – угловое смещение кольца относительно обода,
– угловое смещение кольца относительно обода, 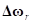 – угловая скорость смещения кольца относительно обода.
– угловая скорость смещения кольца относительно обода.
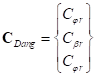 ,
, 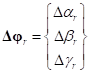 ,
, 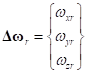 ,
,где 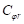 – коэффициент жесткости углового смещения кольца;
– коэффициент жесткости углового смещения кольца;
Тогда упругая составляющая суммарного вектора моментов сил определяется по формуле:
Демпфирующая составляющая суммарного вектора момента сил определяется следующим образом: