1.2.4 Расширенная модель Герца 2
Контакт Герца с постоянным коэффициентом восстановления. Шаблон определяет параметры модели нормального взаимодействия тел.Синтаксис метода создания
extendedHertz2 (deltaU, fU, m, e, nU=…, nDV=…, nDP=…)
Обязательные позиционные параметры метода
scalar deltaU [length]
Характерное значение деформации для определения упругой компоненты силы. Положительная величина.
scalar fU [force]
Величина упругой компоненты силы контактного взаимодействия, соответствующая деформации deltaU. Неотрицательная величина.
scalar m [mass]
Характерная эквивалентная масса соударяемых тел.
scalar e [-]
Коэффициент восстановления скорости. Значение не должно превышать 1 и не должно быть меньше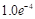 
.
.Необязательные именованные параметры метода
nU = scalar [-]Показатель степени модуля деформации при расчете упругой составляющей. Значение nU должно быть положительным. По умолчанию nU =3/2.
nDV = scalar [-]Показатель степени модуля скорости деформации при расчете вязкой составляющей. Значение nDV должно быть неотрицательным. По умолчанию nDV =1.
nDP = scalar [-]Показатель степени модуля деформации при расчете упругой составляющей. Значение nDP должно быть неотрицательным. По умолчанию nDP =1/4.
Описание
Данная модель относится к семейству вязкоупругих моделей ударного взаимодействия, описание которых приведено в пункте «Общее описание» текущего раздела.
|
Для определения нормальной контактной силы используется модель Герца с постоянным коэффициентом восстановления скорости:
,
,где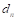 
– проекция деформации на нормаль, положительный скаляр.
– проекция деформации на нормаль, положительный скаляр.Обобщение на случай расчета силы трения:
,
,где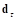 
– проекция деформации на касательную плоскость, двумерный вектор;
– проекция деформации на касательную плоскость, двумерный вектор;
– проекция вектора деформации на вектор 
.Параметр взаимодействия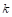 
определяется по заданному пользователем характерному значению деформации и соответствующей величине силы:
определяется по заданному пользователем характерному значению деформации и соответствующей величине силы:
.Параметр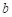 
определяется численно из условия соблюдения установленного пользователем значения коэффициента восстановления скорости.
определяется численно из условия соблюдения установленного пользователем значения коэффициента восстановления скорости.Характерная эквивалентная масса соударяемых тел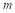 
вычисляется по формуле:
вычисляется по формуле:
,где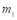 
, 
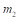– массы соударяемых тел.
, – массы соударяемых тел.Коэффициент восстановления скорости:
,где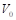 
– нормальная скорость соударения перед ударом,
– нормальная скорость соударения перед ударом,
– нормальная скорость соударения после удара.Значение коэффициента восстановления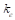 
находится в переделах 
.
находится в переделах 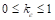.Значение 0 соответствует абсолютно пластическому удару. Это значение недостижимо в рамках вязкоупругих моделей ударного взаимодействия.
Значение 1 соответствует абсолютно упругому удару.