2.1 Силовое взаимодействие точка-поверхность
 Элемент описывает контактное взаимодействие между точкой и поверхностью. Поверхность является ориентируемой, направление нормали определяет сторону поверхности, для которой будет происходить контактное взаимодействие. Направление нормали определяется в рамках метода создания поверхности. Силовое взаимодействие определяется в предположении, что поверхность является наружной поверхностью некоторого тела (звена). Материал этого тела расположен со стороны внутренней поверхности. Силовое взаимодействие возникает при внедрении точки внутрь поверхности, то есть, если точка находится в материале тела, ограниченного поверхностью. Схематический вид элемента представлен на рис. 1.
Элемент описывает контактное взаимодействие между точкой и поверхностью. Поверхность является ориентируемой, направление нормали определяет сторону поверхности, для которой будет происходить контактное взаимодействие. Направление нормали определяется в рамках метода создания поверхности. Силовое взаимодействие определяется в предположении, что поверхность является наружной поверхностью некоторого тела (звена). Материал этого тела расположен со стороны внутренней поверхности. Силовое взаимодействие возникает при внедрении точки внутрь поверхности, то есть, если точка находится в материале тела, ограниченного поверхностью. Схематический вид элемента представлен на рис. 1.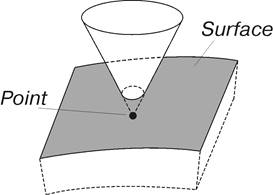
Рис. 1. Силовое взаимодействие точка-поверхность
Силовое взаимодействие происходит только с изображаемой частью поверхности.
Точка и поверхность обязательно должны быть прикреплены к звеньям механической системы. Звено, к которому прикреплена точка, будем называть первым звеном. Звено, к которому прикреплена линия, будем называть вторым звеном.
Данный силовой элемент может быть использован и для расчета контактного взаимодействия между сферой и поверхностью. Для этого необходимо определить необязательный именованный параметр RC – радиус контактирующей сферы; заданная пользователем точка Point при этом интерпретируется как центр этой сферы.
|
Синтаксис метода создания
contactPS2 (Point, Surface, ContactParameters, RC=…, work=..., color=..., visible=...)
Обязательные позиционные параметры метода
point Point
Точка силового взаимодействия.
surface Surface
Поверхность силового взаимодействия.
template ContactParameters
Шаблон параметров контактного взаимодействия.
Необязательные именованные параметры метода
 RC = scalar [length]
RC = scalar [length]Радиус контактирующей сферы с центром в точке Point. Нулевому значению радиуса соответствует точка. По умолчанию RC = 0 [m].
Параметры являются общими для всех методов создания силовых элементов и описаны в пункте «Необязательные именованные параметры всех методов создания» общей части раздела «Силовой элемент (force)» главы «Основные объекты».
Описание
При расчете силового взаимодействия проверяется наличие контакта точки Point и поверхности Surface. Для этого ищется ближайшая к точке Point точка  на поверхности Surface. Если точка
на поверхности Surface. Если точка  не принадлежит изображаемой части поверхности Surface, то считается, что контакта нет. Далее определяется нормаль
не принадлежит изображаемой части поверхности Surface, то считается, что контакта нет. Далее определяется нормаль 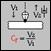 к поверхности в точке
к поверхности в точке  . Если вектор, направленный от точки
. Если вектор, направленный от точки  к точке Point, противоположен вектору
к точке Point, противоположен вектору  , то считается, что контакт есть.
, то считается, что контакт есть.
Расчетная схема силового элемента представлена на рис. 2. При наличии контакта определяются следующие параметры, которые используются для вычисления сил:
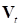
Рис. 2. Расчетная схема силового элемента
Вектор силы, действующей на точку 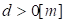 первого звена, равен сумме двух составляющих:
первого звена, равен сумме двух составляющих:
где 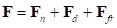 – вектор силы нормальной реакции;
– вектор силы нормальной реакции;
Момент, действующий на точку 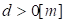 , равен нулю.
, равен нулю.
Сила нормальной реакции направлена по вектору  . Ее значение определяется следующим образом:
. Ее значение определяется следующим образом:
где расчетные формулы для 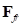 и
и 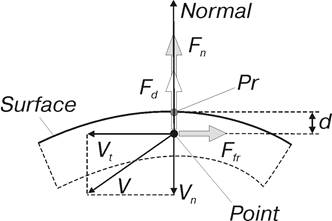 определяются типом заданного пользователем шаблона контактного взаимодействия.
определяются типом заданного пользователем шаблона контактного взаимодействия.
Внутренние системные объекты
sensor gap [length]
Датчик зазора. Выдает знаковое расстояние в контактной паре, положительное при отсутствии контакта и отрицательное при его наличии.
sensor delta [length]
Глубина контакта. Если контакта нет, то датчик выдает нулевое значение.
Корректный вход в контакт
Для корректной работы силового элемента пользователь должен следить за тем, чтобы контакт точки и поверхности осуществлялся только с наружной стороной поверхности.
На рис. 3 представлена корректная реализация модели взаимодействия точки маятника с поверхностью. Точка на маятнике вступает во взаимодействие с поверхностью с внешней стороны. Возникающая сила контактного взаимодействия противодействует свободному движению маятника и стремится придать ему обратный импульс.
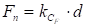 Рис. 3. Корректная реализация модели силового взаимодействия точка-поверхность
|
Некорректная реализация контактного взаимодействия
На рис. 4 представлена некорректная реализация модели взаимодействия точки маятника с поверхностью. Точка на маятнике вступает во взаимодействие с поверхностью с внутренней стороны. В таком ситуации, в текущей реализации для подавляющего большинства расчетных случаев точка пройдет сквозь поверхность, однако в общем случае корректное механическое поведение в результате подобного взаимодействия не гарантируется.
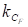 Рис. 4. Некорректная реализация модели силового взаимодействия точка-поверхность
|