7.5 Упругие силы радиальной деформации шины
Согласно схеме взаимодействия колеса с опорной поверхностью (рис. 9) шина связывается с кольцом брекера, соответственно, для расчета упругих сил радиальной деформации должны использоваться параметры положения кольца. В моделях колеса «шина-EULER-M1» и «шина-EULER-M2» звено кольца брекера жестко связывается со звеном обода. Расчет упругих сил радиальной деформации шины производится в предположении, что на каждый дискретный элемент шины, имеющий ненулевой объем деформации, действует упругая сила радиальной деформации, как это представлено на рис. 9 и рис. 10. Эту силу далее будем называть элементарной.
Элементарная сила прикладывается в окрестности точки пересечения оси элемента с опорной поверхностью. Детально это определено в конкретных моделях шины. Вектор элементарной силы располагается в меридиональной плоскости элемента и перпендикулярен линии пересечения этой плоскости с опорной поверхностью.
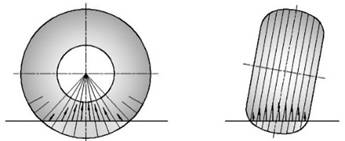
Рис. 9. Элементарные силы упругой радиальной деформации шины
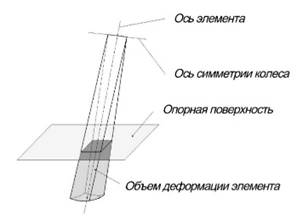
Рис. 10. Дискретный элемент шины
В средней плоскости каждой цилиндрической секции строится линия пересечения секции с опорной поверхностью.
Для каждого сектора в пределах каждой цилиндрической секции определяется объем деформации
,где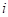 
– номер цилиндрической секции шины;
– номер цилиндрической секции шины;
– номер сектора шины;
– площадь деформации -го сектора в центральной плоскости -ой цилиндрической секции (рис. 11а);
– ширина цилиндрической секции (рис. 11б).Затем определяется объем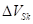 
деформации сектора по всей ширине шины, площадь 
деформации сектора и боковое смещение центра площади 
:
деформации сектора по всей ширине шины, площадь 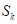деформации сектора и боковое смещение центра площади :
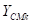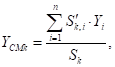
где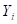 
– боковое смещение средней плоскости -й цилиндрической секции вдоль оси вращения кольца;
– боковое смещение средней плоскости -й цилиндрической секции вдоль оси вращения кольца;
– площадь деформации 
-го сектора -ой цилиндрической секции в плоскости биссектрисы центрального угла сектора.После этого вычисляется суммарный объем деформации шины
.
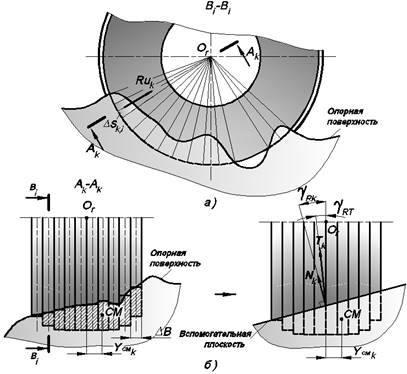
Рис. 11. Расчет взаимодействия с опорной поверхностью произвольной формы
В каждом секторе строится вспомогательная плоскость, перпендикулярная его бисекторной плоскости и расположенная таким образом, что площадь деформации и боковое смещение центра площади, отсекаемой от сектора исходной поверхностью и вспомогательной плоскостью, равны между собой (рис. 11б). Угол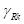 
наклона нормали 
вспомогательной плоскости к оси симметрии поперечного сечения сектора и расстояние 
от центра кольца до вспомогательной плоскости определяются по зависимостям (25), (26) из «Предварительные вычисления вспомогательных зависимостей»:
наклона нормали 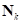вспомогательной плоскости к оси симметрии поперечного сечения сектора и расстояние 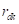от центра кольца до вспомогательной плоскости определяются по зависимостям (25), (26) из «Предварительные вычисления вспомогательных зависимостей»:
; 
По зависимости (22), из того же пункта, определяется объемная плотность статической реакции опорной поверхности
.Предполагается, что нормальная реакция опорной поверхности в 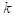-м секторе шины направлена по вектору нормали вспомогательной плоскости. Величина упругой составляющей силы нормальной реакции опорной поверхности в -м секторе шины определяется по формуле:
-м секторе шины направлена по вектору 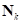нормали вспомогательной плоскости. Величина упругой составляющей силы нормальной реакции опорной поверхности в 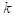-м секторе шины определяется по формуле:
.Функция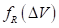 
определяется из условия 
при деформации колеса плоской опорной поверхностью и нулевом угле наклона кольца. Такой расчет обеспечивает физически правдоподобную картину распределения упругих сил радиальной деформации шины. При деформации колеса плоской опорной поверхностью и нулевом угле наклона кольца обеспечивается совпадение полученных сил с задаваемой исходной характеристикой 
. При деформации колеса в промятой колее и наличии ненулевого угла между продольной осью кольца и осью колеи силы упругой радиальной деформации шины создают не только результирующую силу нормальной реакции, но и момент поворота колеса вокруг вертикальной оси.
определяется из условия 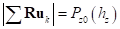при деформации колеса плоской опорной поверхностью и нулевом угле наклона кольца. Такой расчет обеспечивает физически правдоподобную картину распределения упругих сил радиальной деформации шины. При деформации колеса плоской опорной поверхностью и нулевом угле наклона кольца обеспечивается совпадение полученных сил с задаваемой исходной характеристикой 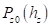. При деформации колеса в промятой колее и наличии ненулевого угла между продольной осью кольца и осью колеи силы упругой радиальной деформации шины создают не только результирующую силу нормальной реакции, но и момент поворота колеса вокруг вертикальной оси.Также для определения точек приложения статических реакций в 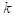-ом секторе рассматривается угол 
и вектор 
перемещений элементов протектора, при которых отсутствуют их касательные деформации, составляющий с центральной плоскостью вращения угол 
. Параметр 
– эмпирический коэффициент. При 
вектор направлен по центральной плоскости шины, при 
– по нормали к опорной плоскости. В модели принято 
.
-ом секторе рассматривается угол 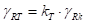и вектор 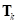перемещений элементов протектора, при которых отсутствуют их касательные деформации, составляющий с центральной плоскостью вращения угол 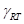. Параметр 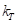– эмпирический коэффициент. При 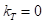вектор 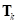направлен по центральной плоскости шины, при 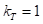– по нормали к опорной плоскости. В модели принято 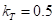.Главный вектор статических реакций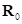 
опорной поверхности в центре кольца определяется как сумма всех упругих составляющих:
опорной поверхности в центре кольца определяется как сумма всех упругих составляющих:
.Для определения значений силовых и кинематических параметров колеса в каждом его положении строится эквивалентная плоскость таким образом, чтобы вектор ее нормальной статической реакции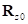 
совпадал с главным вектором сил статических реакций исходной опорной поверхности:
совпадал с главным вектором сил статических реакций 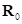исходной опорной поверхности:
.Нормаль эквивалентной плоскости направлена по суммарному вектору упругой составляющей сил нормальной реакции опорной поверхности, действующей на кольцо. Отсюда определяется угол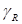 
наклона кольца к эквивалентной плоскости.
наклона кольца к эквивалентной плоскости.Расстояние от центра кольца до эквивалентной плоскости – динамический радиус кольца вычисляется следующим образом:
,
в соответствии с 
в соответствии с Согласно определению эквивалентной плоскости:
.Центр пятна контакта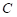 
определяется как проекция центра объема деформации на эквивалентную плоскость.
определяется как проекция центра объема деформации на эквивалентную плоскость.