9 Идентификация

Команда идентификации предназначена для определения значений контрольных параметров в модели исследуемой системы, при которых характеристики поведения модели наилучшим образом соответствуют имеющимся результатам измерения функционирования эталонной системы. Эталонной системой может быть реальная система, т.е. результаты натурных испытаний, или некоторый, в том числе теоретический, прототип этой системы.

Сама задача идентификации, по сути, представляет собой задачу минимизации разницы между значениями выходных характеристик эталонной модели и соответствующих выходных характеристик, полученных в ходе компьютерного моделирования, как функции от вектора входных (идентифицируемых) параметров с учетом их априорного распределения. Сравниваемые характеристики могут быть скалярами, функциями одного аргумента или синтетическими характеристиками, заданными через другие замеренные характеристики.

Для проведения исследования задается следующая исходная информация:

− Идентифицируемые параметры модели, их начальные значения и масштабный коэффициент. Идентифицируемыми параметрами могут быть параметры конструкции, начальные условия движения или любые другие параметры, влияющие на результаты компьютерного моделирования работы исследуемой системы. Опционально можно указать левую и правую границу диапазона значений параметра и априорные статистические характеристики нормального распределения значений параметра (математическое ожидание и дисперсия). Если статистические характеристики не указаны, то распределение считается равномерным. Идентифицируемые параметры модели должны быть типа скаляр (scalar).

− Данные для сравнения выходных характеристик – функций. Включают в себя эталонную выходную характеристику, расчетную выходную характеристику, аргумент и границы его значений, коэффициент эквивалентности и число точек для сравнения. Выходными характеристиками – функциями могут быть кинематические параметры движения (положения, скорости, ускорения) или приборные измерения (направление на объект, угловая скорость радиус-вектора, расход топлива). Эталонные характеристики должны иметь тип функция (function), расчетные характеристики и их аргумент должны иметь тип датчик (sensor).

− Данные для сравнения выходных характеристик – значений. Включают в себя эталонную выходную характеристику, расчетную выходную характеристику и коэффициент эквивалентности. Выходными характеристиками – значениями может быть, например, конечное положение или скорость аппарата или пройденное расстояние. Эталонные характеристики должны иметь тип скаляр (scalar), расчетные характеристики должны иметь тип датчик (sensor).

− Параметры настройки для работы алгоритма оптимизации, а именно метод оптимизации, максимальное число итераций и относительную погрешность.

− Команда расчета процесса функционирования ММС, для которого проводится исследование. В качестве такой команды может использоваться Расчет динамики движения, Расчет сил и ускорений, Расчет траектории положений и другие. Для расчета нельзя применять сложные команды, например, Исследование методом Монте-Карло, Параметрический анализ, Комплексная оптимизация и другие, а также команды, в которые они входят.

− Ограничения в виде уравнения или неравенства (опционально).

Для решения задачи идентификации требуется найти минимум критерия соответствия, который имеет следующий вид:

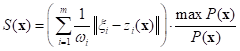где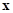

– вектор идентифицируемых параметров;

– число исследуемых характеристик;

– коэффициент эквивалентности

-й характеристики идентификации, имеет ту же размерность, что и сама характеристика, а его значение определяет важность этой характеристики;

– значение

-ой характеристики идентификации в эталонной системе;

– значение

-ой характеристики идентификации в модели динамической системы.

– априорная плотность вероятности распределения значений вектора идентифицируемых параметров.

Если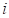

-я характеристика идентификации является функцией, то последовательность значений ее аргумента должна быть монотонна. Норма разности характеристики идентификации эталонной системы и модели динамической системы в данном случае вычисляется с помощью следующей метрики:

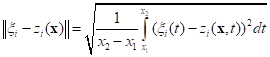где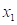

- нижняя и верхняя граница изменения аргумента данной характеристики.

Поиск минимума критерия соответствия осуществляется с помощью указанного метода оптимизации с заданными параметрами. Для решения задачи идентификации предлагается 5 методов поиска экстремума:

− метод Нелдера-Мида;

− стохастический метод (CMA-ES);

− метод сопряженных градиентов;

− метод внутренней точки (IPOPT);

− метод Левенберга-Марквардта.

Для разрешения ограничений, если они указаны, используется расширенный метод множителей Лагранжа.

При каждом вычислении значения критерия соответствия производится расчет процесса функционирования ММС. Во время каждого расчета выполняются следующие действия. Перед изменением значений исходных параметров проект переводится в режим редактирования. После этого меняются значения параметров, и проект переводится в режим исследования. В этот момент проводятся все проверки проекта на корректность и выполняются начальные условия. Затем производится расчет выбранной команды.

Результатом выполнения команды является такой вектор значений идентифицируемых параметров, при котором достигается минимум вышеуказанного критерия соответствия. Также можно посмотреть сравнение эталонных и расчетных выходных характеристик, эволюцию значений идентифицируемых параметров и эволюцию значений параметров характеристик оптимальности (критерия соответствия, критерия оптимальности выбранного метода и критерия выполнения ограничений).