6.3 Напряжённо-деформированное состояние (НДС) при растяжении пластины с отверстием

В данном примере будет исследована точность определения НДС в ПК EULER в окрестности отверстий на упругой модели. В качестве объекта исследования выступает пластина с отверстием, изображенная на рис. 11.

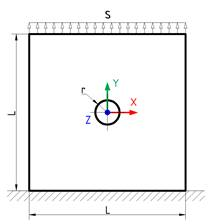
Рис. 11. Испытание упругой пластины с отверстием

Параметры пластины:

− L=0.15 [m] – длина стороны пластины;

− h=0.005 [m] – толщина пластины;

− E=121 10⁹ [Pa] – модуль упругости материала;

− mu=0.39 – коэффициент Пуассона;

− ro=7800 [kg/m³] – плотность материала.

В испытании упругой модели пластины в среде EULER нижняя грань будет зафиксирована, а верхняя грань плавно перемещаться вверх на расстояние S = 0.2 [mm]. Испытание в будет проведено с двумя КЭ-моделями. mnf-файл первой модели создан в ANSYS APDL 18.2 элементами SOLID 185, интерфейсные узлы соединяются с КЭ-сеткой элементами CERIG. А mnf-файл второй модели создан в PATRAN 2012 элементами CTETRA10, интерфейсные узлы соединены с гранями элементами RBE2 «spider». В обоих моделях при формировании КЭ-модели вводиться сгущение сетки вблизи отверстия, для получения более точных результатов. Результаты расчета, а именно распределение полей деформаций и напряжений по пластине, а также значения максимальных напряжений и деформаций будут сравниваться с результатами, полученными в КЭ-комплексе ANSYS APDL 18.2.

Дополнительно будет исследовано влияние количество числа отобранных форм упругого тела на точность и время расчета.

При формировании mnf-файла в обоих случаях использовалось 100 собственных форм упругой модели. Следовательно, в каждом файле будут записаны 106 обобщенных форм. Проведем ряд испытаний, с разным числом обобщенных форм упругого тела. Более подробная информация по формированию mnf-файла, efb-файла и процедуре отбора числа обобщенных форм описана в главах «Формирование исходной и редуцированной моделей в КЭ-комплексах» и «Импорт редуцированной модели в ПК EULER».

В первую очередь стоит отобрать достаточное число форм упругого тела для анализа конструкции. В таблица 2 сведены результаты испытаний упругого тела с разным числом обобщенных форм. Для исследования использовалась первая модель, созданная в ANSYS APDL 18.2. В качестве метода интегрирования использовался метод Рунге-Кутта 4-го порядка с постоянным шагом интегрирования.

Таблица 2. Сводная таблица испытаний КЭ-модели пластины с отверстием

№	Число форм, (ограничение на частоты обобщенных форм)	Максимальное нормальное напряжение по Y, [МПа]	Максимальная линейная деформация по Y,	Время расчета, [s]	Максимальный шаг интегрирования, [s]
1	29 ( < 4000 [Hz])	7961.75	91.461	6.4
2	48 ( < 6000 [Hz])	394.15	3.283	18.3
3	74 ( < 9000 [Hz])	319.18	2.644	37.5
4	101 ( < 12000 [Hz])	238.64	1.976	123.8
5	104 ( < 20000 [Hz])	238.64	1.976	127.0
6	9 *	238.64	1.976	18.1

* только обобщенные формы, описывающие деформации в плоскости пластины.

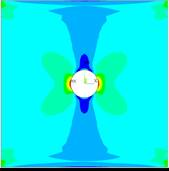
В первом анализе использовалось упругое тело с обобщенными формами до 4000 [Hz]. Форма деформируемый пластины не соответствует предполагаемым результатам, пластина сильно изгибается, вместо растягивания. Если посмотреть на расчетные формы упругого тела, то можно заметить, что там отсутствуют формы, связанные с плоскими деформациями пластины. Следовательно, для данного испытания необходимо использовать формы с более высокими частотами. Формы связанные с изгибом пластины более энергетически выгодны, хотя в данном испытании они практически не проявляются. На рис. 12 показано деформируемое состояние модели в конце расчета.

Рис. 12. Деформируемое состояние упругого тела в первом испытании вид «сбоку»

Во 2-5 расчетах деформируемое состояние соответствует ожиданиям, пластина растягивается. Также заметна сходимость максимальных напряжений и деформаций. На рис. 13 и рис. 14 изображены зависимости максимальных нормальных напряжений и деформаций по оси Y от числа расчетных форм упругого тела. На рис. 15 изображена зависимость времени расчета от числа расчетных форм.

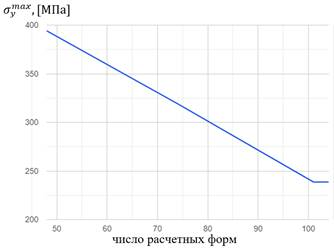
Рис. 13. Максимальное нормальное напряжение по оси Y

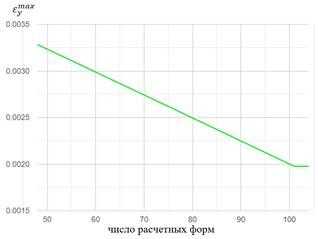
Рис. 14. Максимальная линейная деформация по оси Y

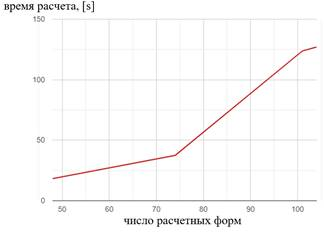
Рис. 15. Время расчета модели испытания

Можно заметить, что использование форм с частотами свыше 12000 [Hz] излишне, так как значения максимальных напряжений и деформаций не изменяются вплоть до 4-й значащей цифры.

В качестве дополнительного исследования был проведен расчет упругого тела с расчетными формами, описывающими только плоские деформации пластины. Результаты анализа приведены в таблица 2 под номером 6. Результаты говорят о том, что при использовании только форм, описывающих деформируемое состояние упругого тела можно достичь той же точности, что и при использовании излишнего числа форм и при этом существенно сократить время расчета. В данном примере время расчета сокращается в 6.8 раз. В сложных конструкциях не всегда есть возможность на раннем этапе избавиться от лишних расчетных форм, особенно в случаях, когда у упругой модели большое число интерфейсных узлов. В таких случаях рекомендуется проводить испытание или несколько испытаний с типовым нагружением и исследовать зависимость выходного параметра от числа расчетных форм, как правило, с увеличением числа форм значение параметра стремится к конкретному числу.

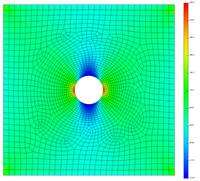
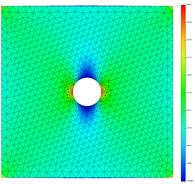
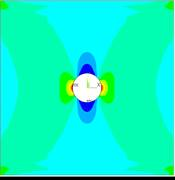
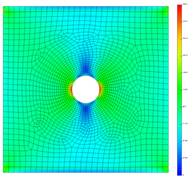
Для проверки НДС пластины с отверстием произведем аналогичный расчет в КЭ-комплексе. В ANSYS APDL 18.2 была создана модель пластины с параметрами, описанными выше. Следует отметить, что КЭ-сетка идентична сетки, используемой при создании редуцированной КЭ-модели для экспорта в EULER. Нижняя грань ограничена на поступательные перемещения по всем 3-м осям. Верхняя грань ограничена на перемещения по осям X и Z. Верхней грани задается перемещение вдоль вертикальной оси Y, равное S=0.2 [mm]. В таблица 3 сведены результаты моделирования растяжения пластины с отверстием в КЭ-комплексе ANSYS APDL 18.2 и в ПК EULER с редуцированными КЭ-моделями, полученными в ANSYS APDL 18.2 и PATRAN 2012. При испытании в EULER использовались упругие тела с расчетными формами до 12000 [Hz]. Внешний вид показан на рис. 16 и рис. 17.



а) ПК EULER КЭ-модель APDL	б) ПК EULER КЭ-модель PATRAN	в) ANSYS APDL

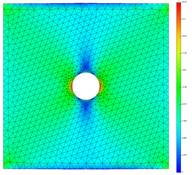
Рис. 16. Поля нормальных напряжений по Y



а) ПК EULER КЭ-модель APDL	б) ПК EULER КЭ-модель PATRAN	в) ANSYS APDL

Рис. 17. Поля эквивалентных напряжений по Мизесу

Таблица 3. Сводная таблица результатов расчета пластины с отверстием

	Максимальное нормальное напряжение по Y, [МПа]	Максимальное эквивалентное напряжение по Мизесу, [МПа]	Максимальная линейная деформация по Y,	Максимальная эквивалентная деформация по Мизесу,
EULER, КЭ-модель APDL	238.64	239.26	1.976	1.832
EULER, КЭ-модель PATRAN	248.20	247.82	2.048	1.898
ANSYS APDL	238.64	239.26	1.976	1.977

Из таблица 3 видно, что редуцированная КЭ-модель в ПК EULER, созданная в ANSYS APDL, в точности совпадает со статическим расчетом в ANSYS. Различия в определении эквивалентных деформаций по Мизесу обусловлены следующим: в mnf-файле (файле редуцированной КЭ-модели) хранятся тензоры напряжений и деформаций по каждой обобщенной форме, а эквивалентные напряжения и деформации для упругого тела определяются, непосредственно, в ПК EULER. В формуле эквивалентных деформаций по Мизесу явно присутствует коэффициент Пуассона:

Значение коэффициента Пуассона в mnf-файл не записывается. Поэтому в ПК EULER эквивалентные значения рассчитываются при одинаковым для всех упругих тел значением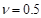

. При моделировании КЭ-модели коэффициент Пуассона был принят равным 0.39. Следовательно, значение эквивалентных деформаций по Мизесу для упругого тела пластины с отверстием в ПК EULER будут связаны с рассчитанными в КЭ-комплексе соотношением:

Отношение максимальной эквивалентной деформации в ПК EULER к значению в КЭ-пакете:



Можно отметить еще одно важное отличие между расчетом в КЭ-комплексе и в ПК EULER в полях эквивалентных напряжений и деформаций. Минимальное значение в ПК EULER всегда принимает значение ноль, а в КЭ-комплексе оно не нулевое. Это связано с тем, что при формировании mnf-файла редуцированной КЭ-модели напряжения и деформации по каждой обобщенной форме записываются только для твердотельных и оболочечных элементов, а в интерфейсном узле (если он не является оболочечным элементом) невозможно определить значения напряжений и деформаций, поэтому там всегда будет ноль. Отсюда и получается минимальное значение эквивалентных напряжений и деформаций равными нулю.

Из таблицы пункта «Напряжённо-деформированное состояние (НДС) при изгибе консольной балки» видно, что результаты расчетов с редуцированными КЭ-моделями из разных КЭ-комплексов заметно отличаются. Это связано с различиями в КЭ-сетках и в способе определения напряжений и деформаций в узлах сетки в разных КЭ-комплексах. Например, в этом примере модель в PATRAN состоит из тетраэдров, элементов «CTETRA10». А в ANSYS APDL из гексаэдров, элементов «SOLID185». К тому же в этих КЭ-комплексах подход к определению деформаций и напряжений отличается, что может приводить к существенным различиям в результатах анализа в ПК EULER. Поэтому при исследовании механических систем с упругими телами в EULER стоит уделять отдельное внимание созданию редуцированной КЭ-модели в специализированных комплексах, от их качества зависит точность получаемых результатов динамического анализа.

Модель испытания:

− Samples\ plate_with_hole\ plate_with_hole.elr

Файлы редуцированных КЭ-моделей:

− plate_NST.mnf – файл, созданный в PATRAN;

− plate_ANS.mnf – файл, созданный в ANSYS APDL.

Модели упругих тел:

− модели по файлу plate_ANS.mnf:

− ANS_4k.efb – с частотами обобщенных форм до 4000 [Hz];

− ANS_6k.efb – с частотами обобщенных форм до 6000 [Hz];

− ANS_9k.efb – с частотами обобщенных форм до 9000 [Hz];

− ANS_12k.efb – с частотами обобщенных форм до 12000 [Hz];

− ANS_20k.efb– с частотами обобщенных форм до 20000 [Hz];

− ANS_FS.efb – с обобщенными формами, плоских деформаций;

− модели по файлу plate_NST.mnf:

− NST.efb – с частотами обобщенных форм до 12000 [Hz].