7.9.2 Расчет реакций опорной поверхности, действующих на кольцо
Расчет упругих составляющих 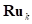 сил нормальных реакций опорной поверхности в
сил нормальных реакций опорной поверхности в  -м секторе шины и расчет эквивалентной плоскости описаны в пункте «Упругие силы радиальной деформации шины».
-м секторе шины и расчет эквивалентной плоскости описаны в пункте «Упругие силы радиальной деформации шины».
Предполагается, что нормальная реакция опорной поверхности в 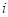 -м цилиндрическом сегменте
-м цилиндрическом сегменте  -го сектора шины направлена по вектору
-го сектора шины направлена по вектору 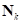 нормали вспомогательной плоскости и приложена в точке
нормали вспомогательной плоскости и приложена в точке  кольца, являющейся проекцией на вспомогательную плоскость вдоль вектора
кольца, являющейся проекцией на вспомогательную плоскость вдоль вектора  контактной точки
контактной точки 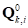 элемента протектора недеформированной шины.
элемента протектора недеформированной шины.
Сила нормальной реакции опорной поверхности с учетом демпфирования в  -м секторе шины вычисляется по формуле (28):
-м секторе шины вычисляется по формуле (28):
где  – проекция скорости кольца брекера в центре объема деформации
– проекция скорости кольца брекера в центре объема деформации  -го сектора шины относительно опорной поверхности на вектор
-го сектора шины относительно опорной поверхности на вектор 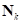 .
.
Величина и вектор упругой составляющей нормальной реакции опорной поверхности в 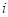 -м цилиндрическом сегменте
-м цилиндрическом сегменте  -го сектора шины определяются следующим образом (рис. 17):
-го сектора шины определяются следующим образом (рис. 17):

где  – расстояние от контактной точки
– расстояние от контактной точки 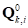 элемента протектора недеформированной шины до вспомогательной плоскости; если
элемента протектора недеформированной шины до вспомогательной плоскости; если 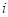 -й цилиндрический сегмент
-й цилиндрический сегмент  -го сектора шины находится не в контакте, то
-го сектора шины находится не в контакте, то 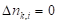 ;
;
Сила нормальной реакции опорной поверхности в  -м секторе шины определяется как равнодействующая сил всех элементов сектора:
-м секторе шины определяется как равнодействующая сил всех элементов сектора:
Момент нормальной реакции опорной поверхности в  -м секторе шины относительно центра кольца определяется по формуле:
-м секторе шины относительно центра кольца определяется по формуле:
где 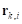 – радиус-вектор точки приложения нормальной реакции в
– радиус-вектор точки приложения нормальной реакции в 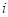 -м цилиндрическом сегменте
-м цилиндрическом сегменте  -го сектора шины.
-го сектора шины.
Главный вектор и главный момент нормальных реакций опорной поверхности в центре кольца определяются по следующим формулам:
Для каждого сектора задается ортогональная система координат 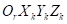 сектора шины, расположенная следующим образом (рис. 18):
сектора шины, расположенная следующим образом (рис. 18):
− центр системы координат сектора находится в центре  кольца;
кольца;
− ось 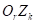 направлена вдоль вектора нормали
направлена вдоль вектора нормали 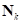 вспомогательной плоскости;
вспомогательной плоскости;
− ось  лежит в плоскости, образованной вектором
лежит в плоскости, образованной вектором 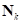 и осью вращения кольца и направлена в ту же сторону, что и ось вращения кольца;
и осью вращения кольца и направлена в ту же сторону, что и ось вращения кольца;
− ось  дополняет систему координат до правой.
дополняет систему координат до правой.
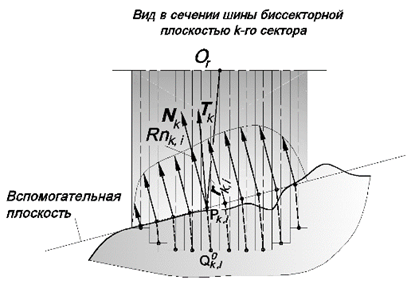
Рис. 17. Распределение нормальных реакций
опорной поверхности в поперечном сечении шины
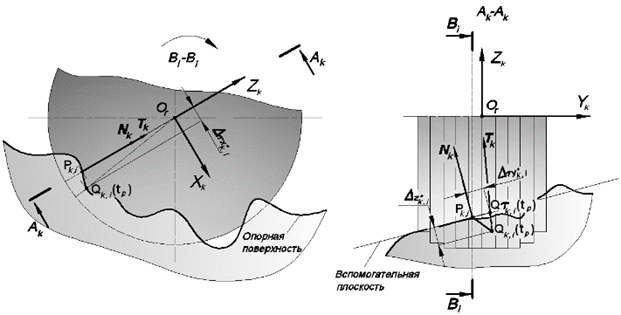
Рис. 18. Деформации протектора 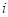 -м цилиндрическом сегменте
-м цилиндрическом сегменте  -го сектора шины
-го сектора шины
Тангенциальные деформации и силы элементов протектора определяются по упругим смещениями контактных точек протектора вдоль осей  и
и  системы координат сектора, а их предельная величина ограничена силой трения между шиной и опорной поверхностью. Ниже приводится алгоритм расчета тангенциальных деформаций и сил элементов протектора:
системы координат сектора, а их предельная величина ограничена силой трения между шиной и опорной поверхностью. Ниже приводится алгоритм расчета тангенциальных деформаций и сил элементов протектора:
где  – проекция на плоскость
– проекция на плоскость 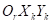 вдоль вектора
вдоль вектора  вычисленной на предыдущем шаге расчета контактной точки
вычисленной на предыдущем шаге расчета контактной точки  элемента протектора в
элемента протектора в 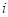 -м цилиндрическом сегменте
-м цилиндрическом сегменте  -го сектора шины (рис. 18);
-го сектора шины (рис. 18);
По предварительным векторам деформаций 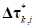 для каждого элемента контакта определяются окончательные вектора деформаций
для каждого элемента контакта определяются окончательные вектора деформаций 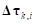 и окончательные вектора сил
и окончательные вектора сил 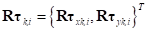 по алгоритму приведенному в пункте 7.7. В качестве жесткостей
по алгоритму приведенному в пункте 7.7. В качестве жесткостей 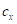 и
и 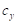 используются жесткости элементов протектора в тангенциальном и осевом направлениях
используются жесткости элементов протектора в тангенциальном и осевом направлениях 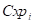 и
и  , а в качестве радиальной деформации
, а в качестве радиальной деформации  используется нормальная реакция опорной поверхности в
используется нормальная реакция опорной поверхности в 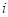 -м цилиндрическом сегменте
-м цилиндрическом сегменте  -го сектора шины
-го сектора шины  . Сила
. Сила 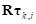 действует на элемент контакта во вспомогательной плоскости и приложена в точке
действует на элемент контакта во вспомогательной плоскости и приложена в точке  . Контактная точка
. Контактная точка 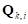 элемента протектора в
элемента протектора в 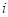 -м цилиндрическом сегменте
-м цилиндрическом сегменте  -го сектора шины на плоскости
-го сектора шины на плоскости 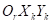 на текущем шаге расчета определяется таким образом:
на текущем шаге расчета определяется таким образом:
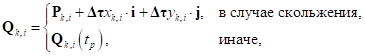
где 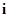 ,
, 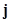 ,
, 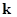 – единичные вектора осей системы координат
– единичные вектора осей системы координат 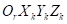 ,
,
При расчете мощности трения скольжения время скольжения 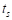 берется
берется
равным  .
.
Сила тангенциальной реакции опорной поверхности в  -м секторе шины определяется как равнодействующая сил всех элементов сектора:
-м секторе шины определяется как равнодействующая сил всех элементов сектора:
Момент тангенциальной реакции опорной поверхности в  -м секторе шины относительно центра кольца определяется по формуле:
-м секторе шины относительно центра кольца определяется по формуле:
где 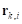 – радиус-вектор точки приложения нормальной реакции в
– радиус-вектор точки приложения нормальной реакции в 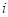 -м цилиндрическом сегменте
-м цилиндрическом сегменте  -го сектора шины.
-го сектора шины.
Главный вектор и главный момент тангенциальных реакций опорной поверхности в центре кольца определяются по следующим формулам: