2.3 Силовое взаимодействие точка-поверхность 2
 Элемент описывает контактное взаимодействие между точкой и поверхностью. Поверхность является ориентируемой. Она имеет наружную и внутреннюю стороны. Нормаль в каждой точке поверхности направлена наружу. Силовое взаимодействие определяется в предположении, что поверхность является наружной поверхностью некоторого тела (звена). Материал этого тела расположен со стороны внутренней поверхности. Силовое взаимодействие возникает при внедрении точки внутрь поверхности, то есть, если точка находится в материале тела, ограниченного поверхностью. На точку контакта действуют следующие силы:
Элемент описывает контактное взаимодействие между точкой и поверхностью. Поверхность является ориентируемой. Она имеет наружную и внутреннюю стороны. Нормаль в каждой точке поверхности направлена наружу. Силовое взаимодействие определяется в предположении, что поверхность является наружной поверхностью некоторого тела (звена). Материал этого тела расположен со стороны внутренней поверхности. Силовое взаимодействие возникает при внедрении точки внутрь поверхности, то есть, если точка находится в материале тела, ограниченного поверхностью. На точку контакта действуют следующие силы:− Сила упругой нормальной реакции со стороны поверхности, ее направление совпадает с направлением нормали поверхности в окрестности внедрения точки.
− Сила нормального демпфирования, вектор силы коллинеарен вектору силы нормальной реакции.
− Сила трения, которая возникает при движении точки вдоль поверхности.
Схематический вид элемента представлен на рис. 11.
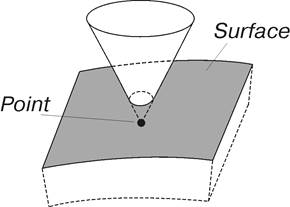
Рис. 11. Силовое взаимодействие точка-поверхность
Силовое взаимодействие происходит только с изображаемой частью поверхности.
Точка и поверхность обязательно должны быть прикреплены к звеньям механической системы. Звено, к которому прикреплена точка, будем называть первым звеном. Звено, к которому прикреплена линия, будем называть вторым звеном.
Данный силовой элемент может быть использован и для расчета контактного взаимодействия между сферой и поверхностью. Для этого необходимо определить необязательный именованный параметр RC – радиус контактирующей сферы; заданная пользователем точка Point при этом интерпретируется как центр этой сферы.
Синтаксис метода создания
contactPS2 (Point, Surface, contactParams, D_max=…, RC=…, work=..., color=..., visible=...)
Обязательные позиционные параметры метода
point Point
Точка силового взаимодействия.
surface Surface
Поверхность силового взаимодействия.
template contactParams
Шаблон параметров контактного взаимодействия. Шаблон должен иметь один из следующих допустимых типов: ПКВ1, ПКВ2, ПКВ3, ПКВ4, ПКВ5.
Необязательные именованные параметры метода
 D_max = scalar [length]
D_max = scalar [length]Предельная глубина контакта. При глубине контакта, превышающей значение этого параметра, силы взаимодействия между точкой и поверхностью обнуляются. По умолчанию D_max = 1 [m].
 RC = scalar [length]
RC = scalar [length]Радиус контактирующей сферы с центром в точке Point. Нулевому значению радиуса соответствует точка. По умолчанию RC = 0 [m].
work =..., color =..., visible =...
Параметры являются общими для всех методов создания силовых элементов и описаны в пункте «Необязательные именованные параметры всех методов создания» общей части раздела «Силовой элемент (force)» главы «Основные объекты».
Описание
При расчете силового взаимодействия проверяется наличие контакта точки Point и поверхности Surface. Для этого ищется ближайшая к точке Point точка 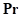 на поверхности Surface. Если точка
на поверхности Surface. Если точка 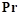 не принадлежит изображаемой части поверхности Surface, то считается, что контакта нет. Далее определяется нормаль
не принадлежит изображаемой части поверхности Surface, то считается, что контакта нет. Далее определяется нормаль 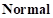 к поверхности в точке
к поверхности в точке 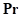 . Если вектор, направленный от точки
. Если вектор, направленный от точки 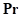 к точке Point, противоположен вектору
к точке Point, противоположен вектору 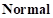 и расстояние между этими точками не превосходит предельной глубины контакта
и расстояние между этими точками не превосходит предельной глубины контакта 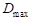 , то считается, что контакт есть.
, то считается, что контакт есть.
Расчетная схема силового элемента представлена на рис. 12. При наличии контакта определяются следующие параметры, которые используются для вычисления сил:
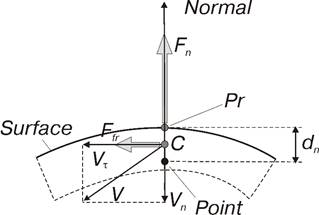
Рис. 12. Расчетная схема силового элемента
Вектор силы, действующей на точку 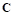 первого звена, равен сумме двух составляющих:
первого звена, равен сумме двух составляющих:
где 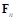 – вектор силы нормальной реакции;
– вектор силы нормальной реакции;
Момент, действующий на точку 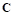 , равен нулю.
, равен нулю.
Сила нормальной реакции направлена по вектору 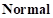 . Ее значение определяется следующим образом:
. Ее значение определяется следующим образом:
где расчетные формулы для 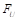 и
и 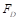 определяются типом заданного пользователем шаблона контактного взаимодействия.
определяются типом заданного пользователем шаблона контактного взаимодействия.
Внутренние системные объекты
sensor distance [length]
Глубина контакта. Если контакта нет или превышена предельная глубина контакта, то датчик выдает нулевое значение.
Расчет трения в контакте
Расчетная схема силы трения представлена на рис. 13. Вязкоупругий элемент трения соединяет точку контакта 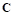 и точку сцепления
и точку сцепления 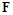 . Обе эти точки могут изменять свое положение в процессе относительного перемещения контактирующих тел. Вектор текущей касательной деформации контакта
. Обе эти точки могут изменять свое положение в процессе относительного перемещения контактирующих тел. Вектор текущей касательной деформации контакта 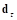 определяется как проекция смещения точки
определяется как проекция смещения точки 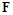 относительно точки
относительно точки 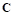 на касательную плоскость контакта
на касательную плоскость контакта
где 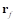 ,
, 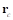 – радиус-векторы точек
– радиус-векторы точек 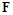 и
и 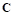 ;
;
Предельное значение касательной деформации контакта определяется силой трения покоя:
где 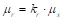 – коэффициент трения покоя.
– коэффициент трения покоя.
Сила трения определяется как сумма упругой и демпфирующей составляющих, которая ограничена силой трения скольжения, если мы находимся в скольжении, или силой трения покоя в противном случае:
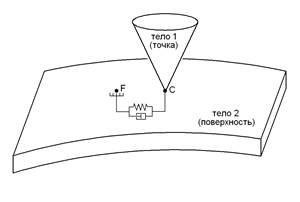
Рис. 13. Расчетная схема силы трения
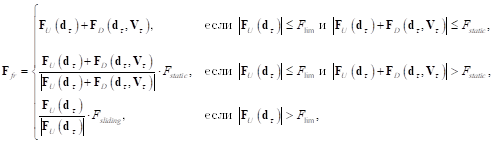
где 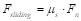 – сила трения скольжения,
– сила трения скольжения,
Страгивание точки сцепления
Если в результате выполнения шага интегрирования выполняется условие 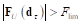 , то считается, что произошло страгивание точки сцепления. Считаем, что предварительное положение точки сцепления до страгивания
, то считается, что произошло страгивание точки сцепления. Считаем, что предварительное положение точки сцепления до страгивания 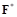 определяется радиус-вектором
определяется радиус-вектором 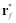 ,
, 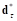 – предварительное значение деформации (до страгивания). Новое положение точки сцепления определяется следующим образом:
– предварительное значение деформации (до страгивания). Новое положение точки сцепления определяется следующим образом:
где 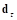 – окончательное значение деформации, определяемое из условия
– окончательное значение деформации, определяемое из условия 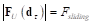 ,
,
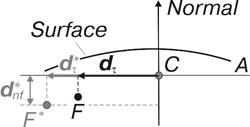
Рис. 14. Страгивание точки сцепления
Корректный вход в контакт
Для корректной работы силового элемента пользователь должен следить за тем, чтобы контакт точки и поверхности осуществлялся только с наружной стороной поверхности, и чтобы глубина контакта не превышала предельного значения.
|
На рис. 15 представлена корректная реализация модели взаимодействия точки маятника с поверхностью. Точка на маятнике вступает во взаимодействие с поверхностью с внешней стороны. Возникающая сила контактного взаимодействия противодействует свободному движению маятника и стремится придать ему обратный импульс.
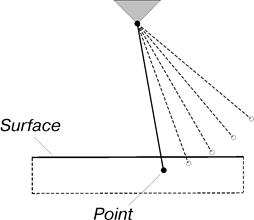 Рис. 15. Корректная реализация модели силового взаимодействия точка-поверхность
|
На рис. 16 представлена некорректная реализация модели взаимодействия точки маятника с поверхностью. Точка на маятнике вступает во взаимодействие с поверхностью с внутренней стороны. Получается физически нереальная картина. Контактное взаимодействие, минуя фазу сжатия, сразу попадает в фазу восстановления. При упругом взаимодействии в этом случае маятнику передается энергия, которая не была накоплена в фазе сжатия, то есть возникает «ниоткуда».
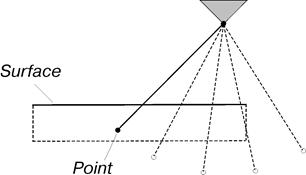 Рис. 16. Некорректная реализация модели силового взаимодействия точка-поверхность
|
Особенности расчета контакта сферы с поверхностью
Если пользователем переопределяется параметр RC – радиус контактирующей сферы с центром в точке Point, то в расчетной схеме элемента под точкой Point понимается внутренняя точка сферы Point*, максимально удаленная от поверхности Surface, т.е. точка сферы соответствующая максимальной глубине контакта (см. рис. 17).
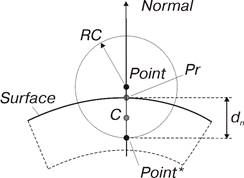
Рис. 17. Иллюстрация использования параметра «радиус сферы»
В случае контакта сферы и поверхности необходима коррекция точки сцепления за счет вращения сферы.
где 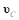 – добавочная скорость (за счет вращения) в точке контакта C;
– добавочная скорость (за счет вращения) в точке контакта C;
Для коррекции вектора текущей касательной деформации контакта 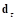 необходимо вычесть смещение за счет вращения:
необходимо вычесть смещение за счет вращения:
где 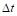 – шаг по времени.
– шаг по времени.
При этом необходимо точку сцепления 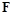 сместить на величину
сместить на величину 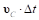 .
.
Для корректной работы на границах поверхности реализован уточненный расчет, схема для которого показана на рис. 18 на примере контакта с плоской поверхностью (для поверхности общего вида – аналогично).
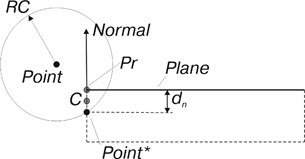 Рис. 18. Расчет контакта на границе на примере плоскости
|
При попадании за границу ищется пересечение с боковой поверхностью, ограничивающей контактирующую поверхность, и точка Point*, соответствующая максимальной глубине контакта (см. рис. 18). В остальном расчет проходит по общей схеме.